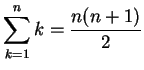
Note that we expect you to be familiar with mathematical induction. If you have not yet seen mathematical induction, you should review the handout discussing it and go to office hours if you have trouble.
The first thing we want to prove today is the equation:
The proof of this is in the induction examples handout. [Note to instructor: you should still show the proof on the board so the students can see the expected format of an induction proof]
Now that we have the basics down, we will use equations similar to the above frequently in our analysis of running times. Recall the formal definition of big-O:
This definition is required when doing a formal proof of running times. Before we get to that, the first step is to write down the recurrence equations for your program. Actually getting the recurrence equations is not a trivial task -- the more complicated the program, the harder it is to figure out. At the basis of it is identifying the atomic operations of the program. This depends on the language you are using, etc. After identifying the atomic operations, you can combine them to determine the recursive calls and the constant values.
From experience and intuition, you know that insertion sort is O(n2), but now we want to prove it. Recall that the recurrence equations for insertion sort are:
Both k1 and k2 are constants. From our discussion of big-O in lecture, you know that an advantage of big-O is classifying programs by obscuring the constants. Since we don't know what k1 or k2 are, we can assume that they are both one. If we did not assume that they are one, we would simply have to scale the analysis accordingly later on. Leaving them as one just makes the whole thing a bit easier. That leaves us with the following recurrence equations for insertion sort:
There are two ways to come about deciding that insertion sort is O(n2): iterative method, and the guess and prove method. (Note other methods do exist, though they do not work for all cases.) First we will try to show insertion sort is O(n2) by the iterative method:
T(n) = T(n-1) + n
= T(n-2) + n-1 + n
= T(n-3) + n-2 + n-1 + n
= T(n-4) + n-3 + n-2 + n-1 + n
...
= T(2) + 3 + 4 + ... + n-4 + n-3 + n-2 + n-1 + n
= T(1) + 2 + 3 + 4 + ... + n-4 + n-3 + n-2 + n-1 + n
= 1 + 2 + 3 + 4 + ... + n-4 + n-3 + n-2 + n-1 + n
Basically, we keep substituting away until we notice a pattern in the iterations. From this we note:
So the running time is explicitly known to be n2 with some constant factors involved. This fits exactly into the high-level definition of O(n2).
The other method is to guess what the big-O set is for the running time and then prove it inductively using the formal definition. So, out of the blue, we're going to say that the big-O running time of insertion sort is O(n2). Let's prove it!
First we choose constants c = 1 and n0 = 1.Property of n to prove
Proof by Induction on n
Base Case: n = 1
T(n) = 1 = 12
Induction Step:
Induction Hypothesis:
for some
Property to prove for n+1:
The above proves the right-hand side of the equation. The left-hand side, 0 <= T(n+1), is obviously true.
Now that we've proven the running times for insertion sort, let's do the same thing for merge sort. Recall that merge sort has the following recurrence relations:
Note again that we really don't need to pay attention to the constants in the equations. The 2 in front of the recursive call to the time equation is important however, so it must remain. That leaves us with the following recurrence equations to work with:
Starting with the iterative method, we can start expanding the time equation until we notice a pattern:
T(n) = 2T(n/2) + n
= 2(2T(n/4) + n/2) + n
= 4T(n/4) + n + n
= 4(2T(n/8) + n/4) + n + n
= 8T(n/8) + n + n + n
= nT(n/n) + n + ... + n + n + n
= n + n + ... + n + n + n
Counting the number of n values in the sum at the end, it is easy to see that there are lg n of them. Thus the time is on the order of n lg n and therefore O(n lg n). So now we've done the analysis by using the iterative method, let's try the guess and prove method.
First we choose constants c = 2 and n0 = 2.Property of n to prove
Proof by strong induction on n
Base case: n = 2
Induction Step:
Induction Hypothesis:
Property to prove for n+1:
It's important to note that big-O actually represents a set. So when we write T(n) = O(n3), we're actually saying that the recurrence equation is an element of the set of functions in O(n3). This also implies that O(n3) is a superset of O(n2). [NOTE: when we ask for big-O on exams and problem sets, we want the smallest big-O set the function is contained in -- otherwise we'll mark it wrong]. Given this knowledge of sets, it is also the case that O(n3 + n2) = O(n3). And it is also the case that O(n3) + O(n2) = O(n3). All this can be proven using the formal definition of big-O shown earlier in section.
Asymptotic efficiency means having the smallest big-O possible. A good example of this is Fast-Fourier Transform (FFT), which is a method for multiplying two polynomials together. The ordinary method for multiplying polynomials is O(n2). FFT involves transforming the polynomials into an intermediate format -- this takes O(n lg n). Pointwise multiplication on this intermediate format is done, which takes O(n) time. Lastly, the resulting pointvalue intermediate format is transformed back into a polynomial representation, which takes O(n lg n) time. Putting this altogether, O(n lg n) + O(n) + O(n lg n) = O(n lg n) which is much better than O(n2).