# Environment Model
This lab focuses on the semantics given in the most recent lecture notes on
[a core sub-language of OCaml](core-ocaml.html).
## Evaluation
In the small-step substitution model, evaluation of an expression was
rather *list-like*: we could write an evaluation in a linear form
like `e --> e1 --> e2 --> ... --> en --> v`. In the big-step environment
model, evaluation is instead rather *tree-like*: evaluations have a
nested, recursive structure. Here's an example:
```
<{}, (3 + 5) * 2> ==> 16 (op rule)
because <{}, (3 + 5)> ==> 8 (op rule)
because <{},3> ==> 3 (int const rule)
and <{},5> ==> 5 (int const rule)
and 3+5 is 8
and <{}, 2> ==> 2 (int const rule)
and 8*2 is 16
```
We've used indentation here to show the shape of the tree, and we've labeled
each usage of one of the semantic rules. A more textbook-style presentation
of that same information would be the following *proof tree*:
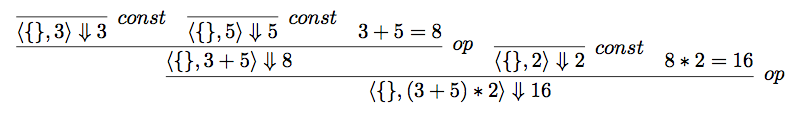
(You can see the \\(\LaTeX\\) source for that image here: [infer.tex](infer/infer.tex).
To avoid requiring everyone in the class to learn \\(\LaTeX\\), though, we will
continue to use a plain ASCII representation of proof trees, as in the first
example above.)
##### Exercise: simple expressions [&#10029;]
Evaluate the following expressions using the big-step environment model.
Use the notation for evaluation that we demonstrated in either of the examples
above, in which you provide a hint as to which rule is applied at each
node in the tree.
- `110 + 3*1000` *hint: three uses of the constant rule, two uses of the op rule*
- `if 2 + 3 < 4 then 1 + 1 else 2 + 2` *hint: five uses of constant, three uses of op,
one use of if(else)*
&square;
##### Exercise: let and match expressions [&#10029;&#10029;]
Evaluate these expressions, continuing to use the tree notation (either
plain text or graphical), and continuing to label each usage of a rule.
- `let x=0 in 1` *hint: one use of let, two uses of constant*
- `let x=2 in x+1` *hint: one use of let, two uses of constant, one use of op, one
use of variable*
- `match Left 2 with Left x -> x+1 | Right x -> x-1` *hint: one use of match(left),
two uses of constant, one use of op, one use of variable*
&square;
##### Exercise: closures [&#10029;&#10029;]
Evaluate these expressions, continuing to use the tree notation (either
plain text or graphical), and continuing to label each usage of a rule.
- `(fun x -> x+1) 2` *hint: one use of application, one use of anonymous function,
two uses of constant, one use of op, one use of variable*
- `let f = fun x -> x+1 in f 2` *hint: one use of let, one use of anonymous function,
one use of application, two uses of variable, one use of op, two uses of constant*
&square;
##### Exercise: lexical scope and shadowing [&#10029;&#10029;]
Evaluate these expressions, continuing to use the tree notation (either
plain text or graphical), and continuing to label each usage of a rule.
- `let x=0 in x + (let x=1 in x)` *hint: two uses of let, two uses of variable,
one use of op, two uses of constant*
- `let x=1 in let f=fun y -> x in let x=2 in f 0` *hint: three uses of let, one use
of anonymous function, one use of application, two uses of variable, three uses of constant*
&square;
##### Exercise: more evaluation [&#10029;&#10029;, optional]
- `let x = 2 + 2 in x + x`
- `let x = 1 in let x = x + x in x + x`
- `let f = fun x -> fun y -> x + y in let g = f 3 in g 2`
- `let f = fst (let x = 3 in fun y -> x, 2) in f 0`
&square;
## Dynamic scope
Recall that dynamically scoped languages use the following evaluation
rules for anonymous functions and function application:
```
<env, fun x -> e> ==> fun x -> e
<env, e1 e2> ==> v
if <env,e1> ==> fun x -> e
and <env,e2> ==> v2
and <env[x->v2],e> ==> v
```
##### Exercise: dynamic scope [&#10029;&#10029;&#10029;]
Use dynamic scope to evaluate the following expression. You do not
need to write down all of the evaluation steps unless you find it
helpful. Compare your answer to the answer you would expect from a
language with lexical scope.
```
let x = 5 in
let f y = x + y in
let x = 4 in
f 3
```
&square;
##### Exercise: more dynamic scope [&#10029;&#10029;&#10029;]
Use dynamic scope to evaluate the following expressions.
Compare your answers to the answers you would expect from a
language with lexical scope.
Expression 1:
```
let x = 5 in
let f y = x + y in
let g x = f x in
let x = 4 in
g 3
```
Expression 2:
```
let f y = x + y in
let x = 3 in
let y = 4 in
f 2
```
&square;
Okay, that's it for the wacky world of dynamic scope.