In a [previous recitation](../22-efficiency/rec.html) you wrote several
recurrence relations describing the running times of several recursive
algorithms. For example, you discovered that
- if $T_c(n)$ gives the running time of `countdown n`, then $T_c(n) ≤ 4S + T_c(n-1)$.
- if $T_f(n)$ gives the running time of `fib n`, then $T_f(n) ≤ 6S + T_f(n-1) + T_f(n-2)$.
- if $T_b(n)$ gives the running time of `bits n`, then $T_b(n) ≤ 4S + T_b(n/2)$.
These equations don't give any obvious way to compare the running times of
these algorithms to those of other algorithms. In this recitation, we will
solve recurrence relations like these to find asymptotic bounds on $T(n)$. We
will see that $T_c$ is $O(n)$, $T_f$ is $O(2^n)$ and $T_b$ is $O(\log n)$.
Proving asymptotic bounds inductively
=====================================
Suppose you are given a recurrence relation (say $T(n) ≤ 4S + T(n-1)$), and
asked to show that $T(n)$ is $O(n)$. You can do an inductive proof using the
definition of big-Oh:
> **Given:** $T(n) ≤ 4S + T(n-1)$
>
> **Claim:** $T(n)$ is $O(n)$, i.e. there exists $c, n_0 > 0$ such that for all
> $n > n_0$, $T(n) ≤ cn$.
>
> **Proof:** Let $c = max(T(1), 4S)$ and let $n_0 = 0$. We will prove the claim by induction on
> $n$.
>
> In the base case, when $n = 1$, we have $T(1) = T(1) \cdot n ≤ cn$, because $c ≥
> T(1)$.
>
> For the inductive step, choose $n > 1$, and suppose $T(n-1) ≤ c(n-1)$ (this
> is the inductive hypothesis). We wish to show that $T(n) ≤ cn$. We have
>
> | | | |
> |------:|-----|:---|:-------|
> |$T(n)$ | $≤$ | $4S + T(n-1)$ | by assumption.|
> | | $≤$ | $4S + c(n-1)$ | by inductive hypothesis.|
> | | $=$ | $cn + (4S-c)$ | |
> | | $≤$ | $cn$ | since $c ≥ 4S$, so $4S-c ≤ 0$ |
>
> as required.
Note that we needed to choose $c$ carefully: we needed $c ≥ T(1)$ for the base
case, and we needed $c ≥ 4S$ in the inductive step; it is not clear how we
chose these. The trick is to do the proof before you choose them, and then go
back and fill in the constants once you know what properties they need to have.
**Exercise**: Given that the running time of `bits` satisfies $T(n) ≤ 4S +
T(n/2)$, prove that $T$ is $O(\log n)$. Note: you will need strong induction,
but otherwise the proof is very similar to the proof above.
**Additional exercises (complete after end of lab):** Prove that `fib n` runs in
time $O(2^n)$. Write a recursive implementation of mergesort and prove that it
runs in time $O(n\log n)$.
Warning!!
---------
Notice that in the proof, we didn't use big-Oh notation; we explicitly expanded
the definition as the very first step.
It is tempting to use big-Oh notation inside the proof, since it is so easy to
work with. **Don't.** The problem is that by using facts about big-Oh in your
inductive step, you can change the constant $c$, so that it depends on $n$.
**Exercise**: explain the flaw in the following "proof":
> **Given:** $T(n) ≤ 2T(n-1)$
>
> **Claim:** $T(n) = O(1)$.
>
> **Proof:** by induction on $n$. Let $n_0 = 0$ and let $c = T(1)$.
>
> In the base case, when $n = 1$, we have $T(n) = T(1) = c$, so $T(1) = O(1)$
>
> For the inductive step, choose $n$, and suppose $T(n-1)$ is $O(1)$. We know
> that $T(n) ≤ 2T(n-1) = 2O(1) = O(1)$, as required.
Deriving asymptotic bounds informally
=====================================
Induction is a good technique for proving $T$ is $O(g)$ once you know $g$, but
how do you derive $g$ in the first place?
A useful technique is to draw the call tree representing the algorithm, and to
determine how much work the algorithm performs at each level.
Consider an algorithm with running time $T(n) ≤ c + 3T(n/2)$. This algorithm
performs some constant time work and then makes three recursive calls with inputs
of size $n/2$. We can draw the call tree for this algorithm:
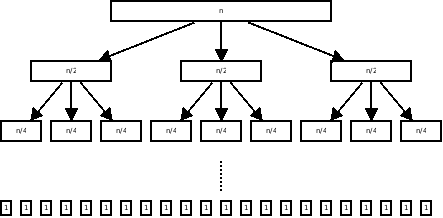
The time spent at the top level (level 0) is $c$ plus the time spent in the
three recursive calls. At the level 1, we spend $c$ time for each of the three
calls, plus the time spent in the 9 recursive calls. Thus we spend $3c$ time
at level 1. Similarly, we spend $9c$ time at level 2, and $3^ic$ time at level
$i$.
The total number of levels is $\log n$, because we split the size in half at
each step. Thus the total time spent is the sum from $i = 0$ to $\log n$ of
$3^i$. This summation [evaluates to $(3^{\log n + 1} - 1)/2$][alpha]
[alpha]: http://www.wolframalpha.com/input/?i=sum+from+i%3D0+to+%28log+n%29+of+3^i
**Exercise**: Merge sort satisfies the recurrence $T(n) ≤ cn + 2T(n/2)$. Use
this technique to derive a formula for running time or merge sort.
The "Master Theorem"
====================
This technique has been generalized into a theorem called the ["Master
Theorem"][master]. It is not worth memorizing the master theorem, but it is
worth knowing how to apply it to a given problem to find an asymptotic bound.
**Exercise**: Use the master theorem to solve the following recurrence
relations:
- $T(n) = 4T(n/2) + n^2$
- $T(n) = 4T(n/2) + n$
- $T(n) = T(n/2) + n^2$
[master]: https://en.wikipedia.org/wiki/Master_theorem#Generic_form