Find an expression that, when substituted for the ??, will cause the following expression to evaluate to 42. Show the evaluation using the substitution model. You may omit minor substitutions, but do show all of the main steps.
let initial x = 0 in
let rec zardoz (f1, lst) =
match lst with
[] -> 3110
| h :: t ->
let f x = h * List.length lst in
if List.length t = 0 then f1 0
else zardoz (f, t) + f 0
in
zardoz (initial, ??)
In this problem you will implement a data compression mechanism called Huffman coding. This is a useful mechanism for compressing data based on the frequencies (number of occurrences) of bytes in a file. The idea is that bytes that occur very frequently are encoded as short bitstrings, while those that occur infrequently are encoded as long bitstrings.
A bitstring is just a sequence of bits, e.g. 10010110. Normally,
printable characters in a file are encoded as bytes, or bitstrings of
length 8. This is called ASCII code. For example, the ASCII code for the character
'a' is the bitstring 01100001, which is binary for 97 decimal.
However, we are not forced to use a fixed-length encoding. If we choose a
different encoding in which the codes can have different lengths, then we can
assign shorter strings to the more frequent characters, thereby saving space.
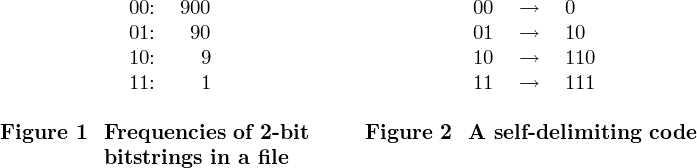
To illustrate, let's do this for bitstrings of length 2. Suppose we have a file that is exactly 2000 bits long. We can view this file as a sequence of 1000 2-bit bitstrings. Suppose we scan the file and find that the four 2-bit bitstrings 00, 01, 10, 11 occur in the file with the frequencies as shown in Fig. 1.

A good encoding for this set of frequencies would be the variable-length code shown in Fig. 2.
This particular encoding has the nice property that it is self-delimiting, which means that no codeword is a prefix of any other codeword. This property allows us to place the codewords end-to-end in a file without having to mark their endpoints, and still be able to recover the original text. For example, if the file begins with
00 00 00 10 10 11 01 00 00 00 00 01...
then it would be encoded as
0 0 0 110 110 111 10 0 0 0 0 10
(We have inserted spaces just to show the original 2-bit bitstrings and the codewords, but the spaces are not really there in the file.) Given the correspondence of Fig. 2, the two sequences determine each other uniquely.
How much space have we saved? The original file was 2000 bits long. The length of the encoded file is
900 · 1 + 90 · 2 + 9 · 3 + 3 = 1110
bits. We have compressed the file by almost half.
A convenient representation of a self-delimiting code is a complete binary
tree with the original uncompressed bitstrings at the leaves. The path from the
root down to the leaf containing x, represented as a bitstring
(left=0, right=1) is the codeword for x. For example, the code of
Fig. 2 would be represented by the tree in Fig. 3. The tree in Fig. 4 shows the
identity code, in which each word is represented as itself. This code
doesn't achieve any compression.


A Huffman tree is a tree built from known frequencies for bitstrings
of some fixed constant length k. It codes frequently
occurring bitstrings of length k as short bitstrings and
infrequently occurring bitstrings of length k as long bitstrings.
The tree of Fig. 3 is a Huffman tree for k=2 constructed from the
frequencies of Fig. 1. In this assignment, you will implement Huffman trees for
k=8 bits (that is, each bitstring is a byte).
To build a Huffman tree, suppose we know the frequency of each
k-bit bitstring in the file. We make a separate tree node for each
k-bit bitstring containing that bitstring as the key along with its
frequency; these will be the leaves of our Huffman tree when we are done. So we
start with a list of 2k single-node trees.
Now we build the Huffman tree bottom up. We repeatedly do the following, while there are at least two nodes in the list:
We keep doing this until there is exactly one element remaining in the list, which is the root of the completed Huffman tree. This has to happen eventually, since the size of the list decreases by one in each stage.
For example, suppose we wish to form a Huffman tree from the frequencies as
shown in Fig. 1. We start with the four tree nodes (00,900),
(01,90), (10,9), (11,1). In the first
stage, the two lowest-frequency elements are x = (10,9) and
y = (11,1). We remove them from the list and
form a new tree node (u,10) with children
(10,9) and (11,1).
Here u is a new key that we assign (see below).
After this step, the list will contain (00,900),
(01,90), and (u,10).
Doing this again, after the next stage the list will contain
(00,900) and (v,100), where v is a new
node with children (u,10) and (01,90). Finally, the
last two nodes are combined, yielding a node (w,1000) which is the
root of the Huffman tree. The resulting Huffman tree looks like Fig. 3.
Lemma: A complete binary tree with n leaves contains
exactly 2n - 1 nodes.
When constructing the tree, you should give each newly constructed internal node a key consisting of a number assigned sequentially, starting at 256 (doing this will help you reconstruct the tree in the decode phase—see below). All the leaves corresponding to ASCII characters will already have keys 0 to 255. By the above lemma, since the root of the tree is the last one constructed, it should always have key value 510. You might want to include this test as a sanity check.
Representation: Choose an appropriate representation
for Huffman trees and define the type huffmantree.
Compression
Huffman codes: Write the function
get_codes : huffmantree -> encoding list.
This function takes a Huffman tree and returns a list of (character, codeword)
pairs. A codeword is represented as an int list, where each int in the list is either
0 or 1. You can implement this function recursively (see Tree
Representation of
Self-Delimiting Codes for a reminder of how this works). When it encounters an
internal node, it recursively finds the list of codes for the left child
and prepends 0 to each, then finds the list of codes for the right
child and prepends a 1 to each, and then combines both lists.
This can be done recursively with only a few lines of code.
Encoding: Write the function
lookup_code : char -> encoding list -> int list.
This function returns the codeword in the encoding list that corresponds to the character.
Now write the function
encode : char list -> huffmantree * int list.
This function takes in text represented as a list of characters and performs Huffman coding on it. It returns the Huffman tree created for the text, along with the encoded text as a list of bits represented as integers.
Saving the Huffman tree: The final compressed file will contain the Huffman tree followed by the sequence of codewords corresponding to the bytes of the input file. We have provided helper functions that write a bitstream to disk (explained below), and in this function you are preparing that bitstream.
Write the function
prepend_tree : huffmantree -> int list -> int list.
This takes a Huffman tree and an existing bitstream and returns a list
with the bit representation of the Huffman tree at the front. The
bit representation of the Huffman tree consists of the keys in
preorder. Add just the keys, nothing else. Use the helper function
Util.to_bits to find the bit representation of each key. You
will be writing an integer, but you only want to write 9 bits of it. (All keys
are less than 512, so they only require 9 bits. We are trying to save space,
remember?)
This can also be done recursively with only a few lines of code.
Longest codeword: Write the function
longest_code : encoding list -> int list.
This will return the longest codeword of all those generated by
get_codes, and must be of length 8 bits or more (can you
explain why?). The Util.write_bits helper function will
use a prefix of that codeword to pad the output file to a multiple of 8 bits.
This step is necessary because file lengths are always in bytes, a multiple of
8 bits. If we just pad out with 0's, we run the risk of adding an extra
unwanted codeword to the end of the file (there might exist a short code
containing all 0s). There is no danger if we use a codeword 8 bits or longer,
because the end of the file will be reached first.
Decompression
Reconstructing the Huffman tree: Before we can decompress, we must reconstruct the Huffman tree that was saved in the compressed file as a preorder sequence of keys. In the decompression phase, the frequencies are not used.
Write the function
regrow_tree : int list -> huffmantree * int list.
This takes a combined bitstream and returns the Huffman tree saved
within it, along with the remainder of the bitstream (without the tree
representation bits). Use the helper function
Util.read_n_bits_to_int to read and process the 9-bit
bitstrings representing the keys in preorder.
Decoding: After reading in the Huffman tree, the remainder of the input bitstream contains the codewords corresponding to the bytes of the uncompressed file.
Write the function
decode : huffmantree -> int list -> char list.
This function returns the character list decoded from the remaining bitstream, based on the given Huffman tree.
We have provided you with helper functions in util.ml. We have
also provided you with the main function which writes the
compressed version of the original file, then decompresses that compressed
version. Make sure you understand what these functions do so you can use them
effectively.
With your Huffman codec, you should see about 25 to 45% compression on large
text files. For very small files, compression will actually make things worse,
because the Huffman tree is stored in the compressed file. We have supplied a
text file text.txt of 213,304 bytes, which our solution code
compresses to 118,576, around 44% compression. You should see comparable
performance, possibly with minor variation depending on your implementation and platform.
For this section of the problem set, you will be implementing a regular expression matcher that supports fuzzy matching of strings. The so-called regular expressions are built using the following constructs.
A lone character is always a regular expression. In our implementation, we only allow lowercase alphabetical characters (i.e. a to z).
# Regexp.accept (Regexp.build "a") "a";; - : bool = trueA fuzzy string {s,k} is a string s accompanied by a number k that matches all strings t such that the Levenshtein distance of s and t is strictly less than k. In short, the Levenshtein distance of two strings is the minimum number of insertions, deletions, or character substitutions it takes to get from one string to the other. Note that there is no space around the comma, and the body s of a fuzzy match must be a plain string, not a general regular expression.
# Regexp.accept (Regexp.build "{hello,3}") "helpoh";;
- : bool = true
Using these two types of regular expressions, we can build more complicated ones. The first way to do so is by concatenation. Simply adjoin two regular expressions to create a new one that matches both in sequence.
# Regexp.accept (Regexp.build "{zardoz,2}{zardoz,2}") "zardozmoardoz";;
- : bool = true
We may also use alternation with the pipe symbol (|) to express a
choice between two regular expressions.
# Regexp.accept (Regexp.build "{help,3}|{me,3}") "derp";;
- : bool = true
# Regexp.accept (Regexp.build "{help,3}|{me,3}") "merp";;
- : bool = true
Finally, we may use the star operator to generate the Kleene closure of a given
regular expression. The regular expression r* matches the
empty string, r, rr, rrr, and so on.
# Regexp.accept (Regexp.build "(hua)*") "huahuahuahuahua";; - : bool = true # Regexp.accept (Regexp.build "a*") "";; - : bool = trueYou may have noticed that we needed to use parentheses in building our regular expressions. The star and alternation operators have higher precedence than concatenation, so ab|cd first matches a, then b or c, and then finally d. The regular expression (ab)|(cd), on the other hand, matches ab or cd.
A nondeterministic finite automaton (NFA) is a construct for implementing a function that takes a string as input and returns true if and only if its input is in a particular set. This set is the language recognized by the NFA. For any legal regular expression, we will formulate a procedure for constructing an NFA whose language is precisely the strings that match the regular expression.
Formally, a NFA is a set of states, an alphabet, a transition relation, a set of start states, and a set of end states. Strings passed as input to the NFA are sequences of characters taken from the alphabet. The transition relation acts as a function that takes the current state and a character from the alphabet as input and returns a set of states. NFAs are naturally depicted as graphs.

The states are the nodes in our graph, and the transition relation provides labeled edges between nodes. Note that for a given state, there can be multiple edges labeled with the same character leaving the node. Additionally, we provide a special transition called an epsilon transition. These edges in the graph represent a "free" edge that can be traversed without consuming a character.
When executing the machine, we would like to step through the input characters one at a time, keeping track of the possible states. However, when we are in the position to consume an input character, a current state of the machine may have an epsilon transition. Taking this path will not consume an input character, but taking other paths may use up the input. Therefore, we would like to not have to worry about epsilon transitions at all. That is, we would like a set of possible states to be epsilon closed, where following an epsilon transition does not leave the set.
Running an NFA steps through the characters of the input string one by one, keeping track of the set of all possible states. Before we have read the input, the machine can be in any of its start states. Next, say S is the set of possible states, and c is the next character of input. Then for each s in S we use the transition relation to lookup the set d(s,c) of all states the machine could be in after reading c while in state s. After doing this for each s, we now have a set of sets of possible states. We then flatten this set to get the next set of possible states. We continue to do this until we run out of characters in the input. Once we are done, we check to see if any of the possible states is also a final state. If so, the string has matched and we return true. Otherwise, we return false.
Given a string s and a maximal edit distance k, we can create an NFA that accepts the set of strings that are less than k edits from s. Here's a NFA that accepts all words within two edits of "food". The following diagram (and the idea for Levenshtein automata) were derived from this blog post.
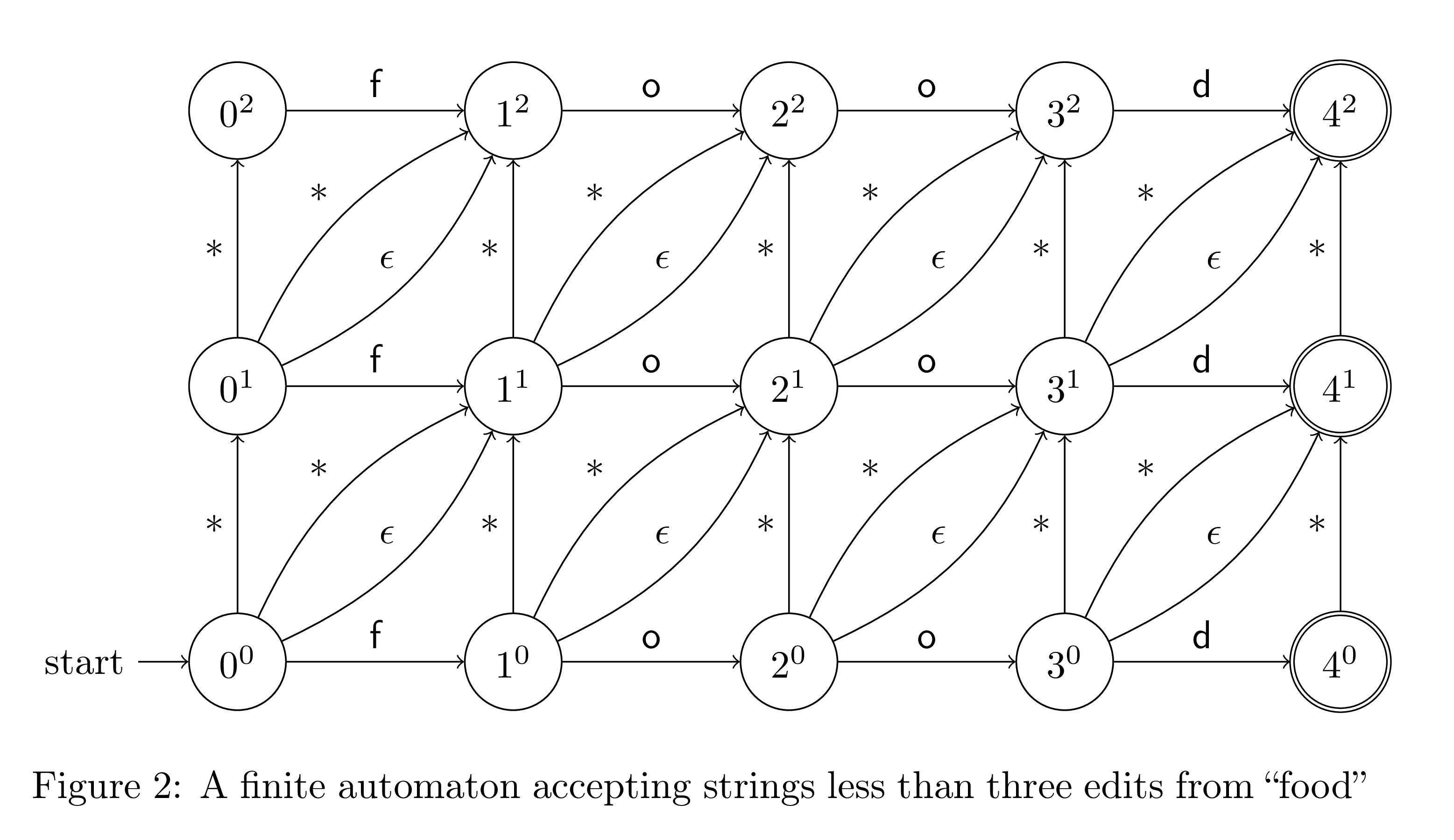
The sole start state is indicated by the arrow, and the three double circle states in the rightmost column are accept states. The states are labeled as ne, where n is the number of characters matched to "food", and e is the number of edits used so far. The horizontal edges represent correct characters in the input string, as we move forward one column while consuming one character of input. The vertical edges are deletions that consume any character and use up one edit without moving forward at all. There are two diagonal transitions, one epsilon transition that does not consume a character and one that consumes any character. The epsilon transition represents inserting the correct character in place, and the consuming transition represents swapping the current character with the correct one. If any of the final states are reached, then we were able to transform the input string to "food" with less than three edits.
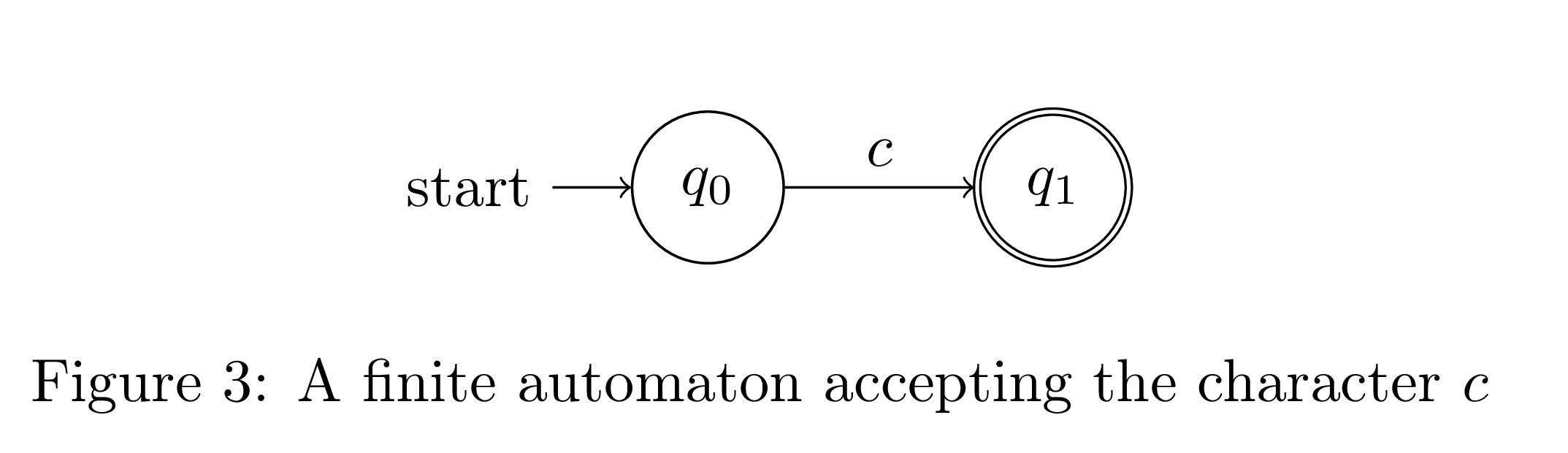
We can also convert any regular expression into an equivalent NFA. We will start by converting simple regular expressions to NFAs. We already implemented fuzzy strings in the previous section, so let's now form an NFA that accepts a single character. We simply have one start state and one end state, and there is one transition connecting them that accepts that character.
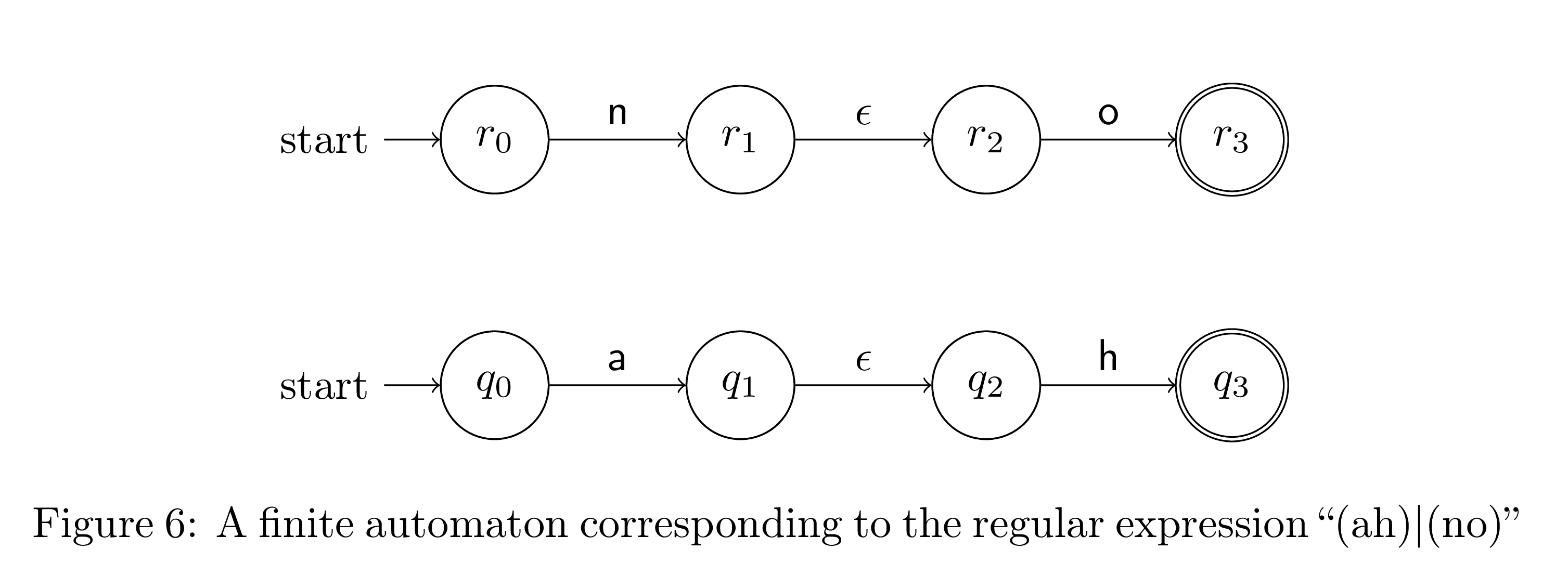
Now let's build our compound regular expressions. We first need to concatenate two regular expressions. One way to do this is to connect every accepting state of the first regular expression to every start state of the second with an epsilon transition. The start states of the first automata are the new start states, and the final states of the second are the new accepting states. Here are two examples of concatenations.


Alternation is trivial. All we have to do is take the union of the start and end states of both automata.
The final case is when we have a star in our regular expression. Consider the case when we have r* for some regular expression r. We have to accept the empty string, so we should first make every start state of r a final state as well. Next, we need to allow for arbitrary repetitions of r. We can do this by connecting every accept state of r to every start state with an epsilon closure.

We have provided a handful of modules for your use in completing this assignment. The first, RegexpUtil provides an abstract syntax tree type regexp for regular expressions and a parser. The second, Util contributes useful functions for generating lists of integers and strings. Finally, the Table module provides an implementation of immutable two-dimensional arrays for storing the transition information. Within the NFA module, we have created StateSet and Dict modules using the OCaml library functors. The interfaces for these modules can be found in the links provided above. We recommend that you familiarize yourself with all of these modules before you start coding.