
Find an expression that, when substituted for the ??, will cause the following function for the given input to evaluate to 42. Show the evaluation using the substitution model. You may omit minor substitutions, but be sure to show all the main steps.
let rec zardoz(f1, n) =
let f(x) = n*(n-1) in
if n = 1 then f1(0)
else zardoz(f, n-1) + f(0)
and initial(x) = 0
in
zardoz(initial, ??)
In this problem you will implement a data compression mechanism called Huffman coding. This is a useful mechanism for compressing data based on the frequencies (number of occurrences) of bytes in a file. The idea is that bytes that occur very frequently are encoded as short bitstrings, while those that occur infrequently are encoded as long bitstrings.
A bitstring is just a sequence of bits, e.g. 10010110. Normally,
printable characters in a file are encoded as bytes, or bitstrings of
length 8. This is called ASCII code. For example, the ASCII code for the character
'a' is the bitstring 01100001, which is binary for 97 decimal.
However, we are not forced to use a fixed-length encoding. If we choose a
different encoding in which the codes can have different lengths, then we can
assign shorter strings to the more frequent characters, thereby saving space.
To illustrate, let's do this for bitstrings of length 2. Suppose we have a file that is exactly 2000 bits long. We can view this file as a sequence of 1000 2-bit bitstrings. Suppose we scan the file and find that the four 2-bit bitstrings 00, 01, 10, 11 occur in the file with the frequencies as shown in Fig. 1.

A good encoding for this set of frequencies would be the variable-length code shown in Fig. 2.
This particular encoding has the nice property that it is self-delimiting, which means that no codeword is a prefix of any other codeword. This property allows us to place the codewords end-to-end in a file without having to mark their endpoints, and still be able to recover the original text. For example, if the file begins with
00 00 00 10 10 11 01 00 00 00 00 01...
then it would be encoded as
0 0 0 110 110 111 10 0 0 0 0 10
(We have inserted spaces just to show the original 2-bit bitstrings and the codewords, but the spaces are not really there in the file.) Given the correspondence of Fig. 2, the two sequences determine each other uniquely.
How much space have we saved? The original file was 2000 bits long. The length of the encoded file is
900 · 1 + 90 · 2 + 9 · 3 + 3 = 1110
bits. We have compressed the file by almost half.
A convenient representation of a self-delimiting code is a complete binary
tree with the original uncompressed bitstrings at the leaves. The path from the
root down to the leaf containing x, represented as a bitstring
(left=0, right=1) is the codeword for x. For example, the code of
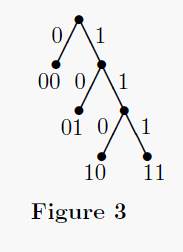
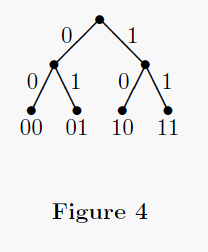
Fig. 2 would be represented by the tree in Fig. 3. The tree in Fig. 4 shows the
identity code, in which each word is represented as itself. This code
doesn't achieve any compression.
A Huffman tree is a tree built from known frequencies for bitstrings
of some fixed constant length k. It tries to code frequently
occurring bitstrings of length k as short bitstrings and
infrequently occurring bitstrings of length k as long bitstrings.
The tree of Fig. 3 is a Huffman tree for k=2 constructed from the
frequencies of Fig. 1. In this assignment, you will implement Huffman trees for
k=8 bits (that is, each bitstring is a byte).
To build a Huffman tree, suppose we know the frequency of each
k-bit bitstring in the file. We make a separate tree node for each
k-bit bitstring containing that bitstring as the key along with its
frequency; these will be the leaves of our Huffman tree when we are done. So we
start with a list of 2k single-node trees.
Now we build the Huffman tree bottom up. We repeatedly do the following, while there are at least 2 nodes in the list that aren't yet part of the Huffman tree:
We keep doing this until there is exactly one element remaining in the list,
which will become the root of the completed Huffman tree. This has to happen
eventually, since the size of the list decreases by one in each stage.
For example, suppose we wish to form a Huffman tree from the frequencies as
shown in Fig. 1. We start with the four tree nodes (00,900),
(01,90), (10,9), (11,1). In the first
stage, the two lowest-frequency elements are x = (10,9) and
y = (11,1). We form a new tree node (u,10) with children
(10,9) and (11,1), and this becomes our working Huffman
tree. Here u is a new key that we assign (see below).
After this step, the list will contain (00,900),
(01,90), and (u,10).
Doing this again, after the next stage the list will contain
(00,900) and (v,100), where v is a new
node with children (u,10) and (01,90). Finally, the
last two nodes are combined, yielding a node (w,1000) which is the
root of the Huffman tree. The resulting Huffman tree looks like Fig. 3.
Lemma: A complete binary tree with n leaves contains
exactly 2n - 1 nodes.
When constructing the tree, you should give each newly constructed internal node a key consisting of a number assigned sequentially, starting at 256. All the leaves corresponding to ASCII characters will already have keys 0 to 255. By the above lemma, since the root of the tree is the last one constructed, it should have key value 510. You might want to include this test as a sanity check.
Representation: Choose an appropriate representation
for Huffman trees and define the type huffmantree.
Compression
Huffman codes: Write the function
get_codes : huffmantree -> encoding list.
This function takes a Huffman tree and returns a list of character to codeword mappings. You can implement this function by recursively walking the tree from the root and outputting partial codeword lists (see Tree Representation of Self-Delimiting Codes for a reminder of how this works). When it encounters a parent node, for example, it finds the list of codes for the left child and prepends 0 to each. It then finds the list of codes for the right child and prepends a 1 to each, and then combines both lists.
This can be done recursively with only a few lines of code.
Encoding: Write the function
lookup_code : char -> encoding list -> int list.
This function returns the codeword in the encoding list that corresponds to the character.
Now write the function
encode : char list -> huffmantree * int list.
This function takes in text represented as a list of characters and performs Huffman coding on it. It returns the Huffman tree created for the text, along with the encoded text as a list of bits represented as integers.
Saving the Huffman tree: The final compressed file will contain the Huffman tree followed by the sequence of codewords corresponding to the bytes of the input file. We have provided helper functions that write a bitstream to disk (explained below), and in this function you are preparing that bitstream.
Write the function
prepend_tree : huffmantree -> int list -> int list.
This takes a Huffman tree and an existing bitstream, and returns a list
with the bit representation of the Huffman tree at the front. The
bit representation of the Huffman tree consists of the keys in
preorder. Add just the keys, nothing else. Use the helper function
Util.to_bits to find the bit representation of each key. You
will be writing an integer, but you only want to write 9 bits of it. (All keys
are less than 512, so they only require 9 bits. We are trying to save space,
remember?)
This can also be done recursively with only a few lines of code.
Longest codeword: Write the function
longest_code : encoding list -> int list.
This will return the longest codeword of all those generated by
get_codes, and must be of length 8 bits or more (can you
explain why?). The Util.write_bits helper function will
use a prefix of that codeword to pad the output file to a multiple of 8 bits.
This step is necessary because file lengths are always in bytes, a multiple of
8 bits. If we just pad out with 0's, we run the risk of adding an extra
unwanted codeword to the end of the file (there might exist a short code
containing all 0s). There is no danger if we use a codeword 8 bits or longer,
because the end of the file will be reached first.
Decompression
Reconstructing the Huffman tree: Before we can decompress, we must reconstruct the Huffman tree that was saved in the compressed file as a preorder sequence of keys. In the decompression phase, the frequencies are not used.
Write the function
regrow_tree : int list -> huffmantree * int list.
This takes a combined bitstream and returns the Huffman tree saved
within it, along with the remainder of the bitstream (without the tree
representation bits). Use the helper function
Util.read_n_bits_to_int to read and process the 9-bit
bitstrings representing the keys in preorder.
Decoding: After reading in the Huffman tree, the remainder of the input bitstream contains the codewords corresponding to the bytes of the uncompressed file.
Write the function
decode : huffmantree -> int list -> char list.
This function returns the character list decoded from the remaining bitstream, based on the given Huffman tree.
We have provided you with helper functions in util.ml. We have
also provided you with the main function which writes the
compressed version of the original file, then decompresses that compressed
version. Make sure you understand what these functions do so you can use them
effectively.
With your Huffman codec, you should see about 25 to 45% compression on large
text files. For very small files, compression will actually make things worse,
because the Huffman tree is stored in the compressed file. We have supplied a
text file text.txt of 213,304 bytes, which our solution code
compresses to 118,576, around 44% compression. You should see equivalent
performance.
A quadtree is a data structure that supports searching for objects located in a two-dimensional space. To avoid spending storage space on empty regions, quadtrees adaptively divide 2D space. Quadtrees are heavily used in graphics and simulation applications for tasks such as quickly finding all objects near a given location and detecting collisions.
There are many variations on quadtrees specialized for different applications. For this problem set, we'll use a variation in which each node represents a rectangular region of space parameterized by x and y coordinates: all the space between x coordinates x0 and x1 and between y coordinates y0 and y1.
A leaf node contains some (possibly empty) set of objects that are all located at the same point (x, y), which must lie within the leaf's rectangle. A non-leaf node has four children, each covering one quarter of the parent node's rectangle, as shown in this picture:

To insert an object at coordinates (x,y), we traverse the quadtree starting from the top node and walk down through the appropriate sequence of child nodes that contain the point (x,y) until we reach a leaf node. This figure depicts the quadtree nodes that we visited in the process of inserting an object located at the black dot.

If the object to be inserted is at the same point as the other objects at that leaf, we can just add it to the leaf's list of objects. Otherwise we must split the leaf into quadrants.
Representation: Document your implementation with a detailed
description of the quadtree data structure in quadtree.ml.
It is up to you how you want to design and specify the quadtree, but be
sure to read the tasks below carefully to give you a good idea of
what operations it should efficiently support.
Operations: Write the functions make, insert, and
fold_rect in the Quadtree module.
City Search: Write the function make_city_quadtree,
which takes a list of cities and returns a quadtree containing the names of
these cities, indexed by their coordinates. Use the load_cities helper
function to load cities from our provided dataset, us-places.txt.
Now write the function city_search, which takes a quadtree
created by make_city_quadtree and a rectangle specifying a region
between a particular latitude and longitude, and returns all cities lying within
that region.
Karma Problem: Implement an alternative way to search for cities,
circle_search which returns all cities within a distance of r of a particular point.
This is tricky to get right; one testing trick is to see if you always match
the answer returned by a reference implementation that is brute-force,
obviously correct, and likely much slower.