Problem Set 2: Folding and Datatypes

Due Thursday September 22, 2011

Version: 10
Last Modified: September 19, 12:34
Changes:

Important notes:

  1. No partners: You are to work alone on this assignment.
  2. Compile errors: All programs that you submit must compile. Programs that do not compile will probably receive an automatic zero. If you are having trouble getting your assignment to compile, please visit consulting hours. If you run out of time, it is better to comment out the parts that do not compile and hand in a file that compiles, rather than handing in a more complete file that does not compile.
  3. Missing functions: We will be using an automatic grading script, so it is crucial that you name your functions and order their arguments according to the problem set instructions, and that you place the functions in the correct files. Otherwise you may not receive credit for a function properly written.
  4. Code style: Please pay attention to style. Refer to the CS 3110 style guide and lecture notes. Ugly code that is functionally correct may still lose points. Take the extra time to think through the problems and find the most elegant solutions before coding them up.
  5. Wrong versions: Please double-check that you are submitting the correct versions of your files to CMS. The excuse, "I had it all done, but I accidentally submitted the wrong files" will not be accepted.

Part 1: List Folding (30 points)

Folding is one of the most useful tools in functional programming. You will certainly use it many times over the course of the semester. The following exercises are designed to get you comfortable with folding to do useful computations on lists. Note: All of these functions can be written without folding, but the point of the exercise is to get used to folding, so every function must include either List.fold_left or List.fold_right. Note that List.fold_left is tail recursive and List.fold_right is not. For full credit, do not use the rec keyword.

  1. (3 points) Write a function fold_map : ('a -> 'b) -> 'a list -> 'b list that is an implementation of the List.map function using only List.fold_left or List.fold_right.
    Example: fold_map succ [1;2;3] = [2;3;4].

  2. (3 points) Using folding, write a function mean : int list -> float that calculates the mean score of all students in the class.

  3. (3 points) Using folding, write a function max2 : int list -> int that returns the second-largest value in the list. Do not sort the list. Fail with an appropriate exception if the list is too short. Note: there may be duplicates in the list, and the second-largest value may be the same as the largest, in which case you should return it. I.e., the result should be the same as if you sorted the list in descending order and took the second element.

  4. (5 points) Using folding, write a function is_palindrome: int list -> bool. Returns true if the given list is a palindrome, false otherwise. You are allowed to use List.rev, but you are NOT allowed to use the OCaml equality test (ie, =) on lists. You are still allowed to use = between individual elements.

  5. (6 points) Using folding, write a function all_prefixes: 'a list -> 'a list list that returns a list of all non-empty prefixes of the given list, ordered from shortest prefix to longest prefix. For example, all_prefixes [1;2;3;4] = [[1]; [1;2]; [1;2;3]; [1;2;3;4]].

  6. (10 points) Write a function mystery_base_addition : int list -> int list -> int -> int list . Given two lists of nonnegative integers in the range 0 to b-1, each representing the base-b (b >= 2) digits of a number from higher to lower significance, you must add the two numbers together.

    Your result must not contain any leading zeroes, but must be able to handle leading zeroes in the inputs.
    You only need to handle cases where base >= 2. Operation is officially undefined for base < 2, so you may do whatever you want in these cases (output a correct result, output an empty list, raise an exception, etc.).

    Example:
    mystery_base_addition [0;0;1] [0;0;1] 2 = [1;0]
    mystery_base_addition [2;7] [1;5] 10 = [4;2]
    mystery_base_addition [8] [1;2] 10 = [2;0]

    You should not assume that valid digits for base b will be passed in and should therefore consider checking for cases where the input contains integers that are not in range. In this case, you should raise InvalidNumber .

    Example: mystery_base_addition [2;7] [1;5] 3 = Exception: InvalidNumber "Higher than base".

    Hint: For this problem, you may find it to useful to use List.fold_left2 or List.fold_right2.

Part 2: Symbolic Differentiation (45 points)

In the Summer of 1958, John McCarthy (recipient of the Turing Award in 1971) made a major contribution to the field of programming languages. With the objective of writing a program that performed symbolic differentiation of algebraic expressions, he noticed that some features that would have helped him to accomplish this task were absent in the programming languages of that time. This led him to the invention of LISP (published in Communications of the ACM in 1960) and other ideas, such as list processing (the name Lisp derives from "List Processing"), recursion and garbage collection, which are essential to modern programming languages, including Java. Nowadays, symbolic differentiation of algebraic expressions is a task that can be conveniently accomplished with modern mathematical packages, such as Mathematica and Maple.

The objective of this part is to build a language that can differentiate and evaluate symbolically represented mathematical expressions that are functions of a single variable x. Symbolic expressions consist of numbers, variables, and standard functions (plus, minus, times, divide, sin, cos, etc). To get you started, we have provided the datatype that defines the abstract syntax for such expressions.

(* abstract syntax tree *)
(* Binary Operators *)
type bop = Add | Sub | Mul | Div | Pow

(* Unary Operators *)
type uop = Sin | Cos | Ln | Neg

type expr = Num of float
          | Var
          | BinOp of bop * expr * expr
          | UnOp of uop * expr

This datatype provides an internal representation of an expression that the user might type in. The constructor Var represents the single variable x, and UnOp (Ln, Var) represents the natural logarithm of x. Neg refers to unary negation and is denoted by the symbol ~. (the symbol - is only used for subtraction). The meaning of the others should be clear. Mathematical expressions can be constructed using the constructors in the above datatype definition. For example, the expression x^2 + sin(~x) would be represented internally as:

BinOp (Add, BinOp (Pow, Var, Num 2.0), UnOp (Sin, UnOp (Neg, Var)))

This represents a tree in which nodes are the type constructors and the children of each node are an operator and the arguments of that operator. Such a tree is called an abstract syntax tree (or AST for short).

For your convenience, we have provided a function parse_expr which translates a string in infix form (such as x^2 + sin(~x)) into a value of type expr. The parse_expr function parses according to the standard precedence of operations, so 5 + x * 8 will be read as 5 + (x * 8). We have also provided two functions to_string and to_string_smart that print expressions in a readable form using infix notation. The former produces a fully-parenthesized expression so you can see how the parser parsed the expression, whereas the latter omits unnecessary parentheses.

# let e = parse_expr "x^2 + sin(~x)";;
val e : Expression.expr =
  BinOp (Add, BinOp (Pow, Var, Num 2.), UnOp (Sin, UnOp (Neg, Var)))
# to_string e;;
- : string = "((x^2.)+(sin((~(x)))))"
# to_string_smart e;;
- : string = "x^2.+sin(~(x))"

For full credit, only use rec in your implementation of fold_expr. Do not use rec in evaluate and derivative.

  1. Write a function fold_expr : (expr -> 'a) -> (uop -> 'a -> 'a) -> (bop -> 'a -> 'a -> 'a) -> expr -> 'a such that fold_expr atom unary binary expr performs a postorder traversal of expr. During the traversal, it applies atom : expr -> 'a to every leaf node (i.e. Var or Num). It applies unary : uop -> 'a -> 'a to every unary expression. The first argument to unary is the unary operator and the second is the result of applying fold_expr recursively to that expression's operand. Finally, fold_expr applies binary : bop -> 'a -> 'a -> 'a to every binary expression. The arguments to binary are the binary operator and the results of recursively applying fold_expr to the left and right operands.
    For example, here is a function that uses fold_expr to determine whether the given expression contains a variable. 
    let contains_var : expr -> bool =
  let atom = function
    | Var -> true
    | _ -> false in
  let unary op x = x in
  let binary op l r = l || r in
  fold_expr atom unary binary

    You may use rec in your implementation of fold_expr without penalty.
  2. Using fold_expr, write a function eval : float -> expr -> float such that eval x e evaluates e, setting Var equal to the value x. For full credit, do not use rec in evaluate.
    Example: eval 2.0 (BinOp (Add, Num 2.0, Var)) = 4.0.
  3. Using fold_expr, write a function derivative : expr -> expr that returns the derivative of an expression with respect to Var. The expression it returns need not be simplified. For full credit, do not use rec in derivative.
    Example: derivative (BinOp (Pow, Var, Num 2.0)) = BinOp (Mul, Num 2., BinOp (Mul, Num 1., BinOp (Pow, Var, BinOp (Sub, Num 2., Num 1.))))

    When implementing this function, recall the chain rule from your freshman calculus course:

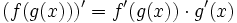
    This rule tells how to form the derivative of the composition of two functions if we know the derivatives of the two functions. With the help of this rule, we can write the derivatives for all the operators in our language:

    There are two cases provided for calculating the derivative of f(x) ^ g(x), one for where g(x) = h does not contain any variables, and one for the general case. The first is a special case of the second, but it is useful to treat them separately, because when the first case applies, the second case produces unnecessarily complicated expressions.

Part 3: Fields of Sets (25 points)

In this section, you're going to write some functions related to data mining applications. Suppose we have some set of items: our goal is to find subsets of this set of item set which are significant.

For full credit, do not use the rec keyword in any portion of part 3: gen_subsets, generate_counts, or find_large_sets.

  1. In order to identify large subsets, we'd like to first list all possible subsets of our base set. Using fold, implement the function gen_subsets: 'a list -> 'a list list which takes a list, and generates a list of all possible subsets of the list. We will call this output the lattice. Don't worry if your solution has a horrifically slow runtime. This is just a way for you to practice using fold. In real data mining applications there are tricks that can be used to speed up this step of the process, but you don't have to worry about those.

  2. Suppose we have collected a set of data, consisting of subsets of the base set. For example, our base set could be a list of musical artists, and each transaction could be the subset of this list that some person likes. By finding which of these subsets occur in many transactions, we will be able to generate rules which associate different elements. For example, we'd expect a subset containing both The Beatles and the Rolling Stones to occur frequently, while a subset containing both Nas and Lady Gaga would be less likely. The first thing we have to do is count how many times each subset occurs.
    Implement the function generate_counts: 'a list list -> 'a list list -> ('a list * int) list which takes the lattice generated from gen_subsets and a list of "transactions" (a transaction is simply a single element of the lattice, though our list of transactions may have repeats of the same element). It returns a list of tuples which reports how many times each subset in the lattice showed up in the list of transactions. For example, the transaction {A,B} would increment the counts for the subsets {A,B}, {A}, {B}, and {}.

    Your output need not be sorted in any particular order, but you must ensure that for every subset in the lattice, there is exactly one corresponding (subset, count) tuple in the result. The individual elements of each subset do not need to stay in the same order either, but there should be only one of each subset. For examples, read the bottom of the page.


  3. Finally, in order to find out how often a subset appears, we have to divide by the total number of transactions.
    Implement the function find_large_sets: ('a list * int) list -> float -> 'a list list which takes the output from generate_counts and a threshold, and returns a list of all elements of the lattice that appear in the list of transactions in a fraction greater than or equal to the threshold. For example, if our set of transactions were {A},{A,B},{A,B,C}, {A,B}, {A,C}, and our threshold was 0.6, {}, {A}, {B}, and {A,B} would be output, but not {C}, {A,C}, {B,C}, or {A,B,C}. 
    let subsets = gen_subsets ['A'; 'B'; 'C'] in
let transactions = [['A']; ['A'; 'B']; ['A'; 'B'; 'C']; ['A'; 'B']; ['A'; 'C']] in
let counts = generate_counts subsets transactions in
find_large_sets counts 0.6
(* [[]; ['A']; ['B']; ['A'; 'B']] *)

Example invocations for generate_counts

Example input 1: 

let lattice = gen_subsets [1; 2];;
(* lattice = [[]; [1]; [2]; [1; 2]], or some equivalent. *)
generate_counts lattice [[1]];;

Acceptable outputs: 

(* Fully sorted output *)
[([], 1); ([1], 1); ([2], 0); ([1; 2], 0)]

(* Okay to reorder the elements in [2; 1] *)
[([], 1); ([1], 1); ([2], 0); ([2; 1], 0)]

(* Okay to put the subsets in any arbitrary order*)
[([2; 1], 0); ([2], 0); ([1], 1); ([], 1)]

Unacceptable outputs: 

(* Where did the counts for [2] and [1; 2] go??? *)
[([], 1); ([1], 1)]

Example input 2: 

let lattice = gen_subsets [1; 2];;
generate_counts lattice [[2; 1]; [1; 2]];;

Acceptable outputs: 

[([], 2); ([1], 2); ([2], 2); ([1; 2], 2)]
[([], 2); ([1], 2); ([2], 2); ([2; 1], 2)]
(* Also, any rearrangement of these (subset, count) pairs is OK *)

Unacceptable outputs: 

(* [1; 2] and [2; 1] are the same set, so they should be combined! *)
[([], 2); ([1], 2); ([2], 2); ([1; 2], 1); ([2; 1], 1)]