
For this problem set, you are to turn in an overview document covering problems 3 and 4. It's your job to convince us that your code works, by describing your implementation and by presenting a testing strategy, test cases, and results. The overview document should be composed as described in Overview Requirements. You should read this document carefully. We have provided an example overview document written as if for Problem Set 2 from CS 312, Spring 2008.
In particular, starting with this problem set, it's your job to convince us that your code works, by describing your implementation and by presenting a testing strategy, test cases, and results.
You may work on this problem set with a partner. We strongly recommend discussing, critiquing, and agreeing on specifications for Parts 3 and 4 before doing any implementation. A nice approach is to have one partner write rough drafts of specs for Part 3, the other partner write rough drafts of specs for Part 4, then to discuss how both specs can be improved. You can also bring specs to office hours to get feedback. This is also a good problem set to try pair programming on, rather than trying to work independently. When critiquing a spec, think about the spec both from the standpoint of the client who is going to use the spec, and the implementer who must implement it. It is also a good idea to discuss and agree on the abstraction function and rep invariant for your data structures.
g in Part 2.
Find an expression that, when substituted for the ??, will cause the following function for the given input to evaluate to 42. Show the evaluation using the substitution model. You may omit minor substitutions, but be sure to show all the main steps.
let rec zardoz(f1, n) =
let f(x) = n*(n-1) in
if n = 1 then f1(0)
else zardoz(f, n-1) + f(0)
and initial(x) = 0
in
zardoz(initial, ??)
Consider the following function specifications for functions
a–h of type
int list->int
. Draw a
Hasse diagram showing
which function specifications refine each other. This diagram should include
a node for each function name. If function spec A refines spec B, the name B
should appear higher in the diagram. Further, there should be a line in the diagram
connecting A and B, unless there is some third spec C where A refines C and C
refines B.
(* a(x) = y, where y is the last element in x. Requires: x contains at least three elements. *) (* b(x) = y, where y is the largest element in x. Requires: x is non-empty. *) (* c(x) = y, where y is the last element in x. Requires: x is non-empty and in ascending sorted order. *) (* d(x) = y, where y is the first element in x. Requires: x is non-empty. *) (* e(x) = y, where y is an element in x. Requires: x is non-empty. *) (* f(x) = y, where y is the last element in x. Requires: x is non-empty. *) (* g(x) = y, where y is the element in x with the largest absolute value. Requires: x is non-empty. *) (* h(x) = y, where y is the largest element in x. Requires: x is non-empty and in descending sorted order. *)
Hint: Spec b refines e and h, so b should lie below both e and h
in the diagram and should be connected to them, perhaps indirectly. Assuming
there is no spec that lies between b and e or between b and h in the refinement
ordering, that part of the diagram would look like this:


The Mystic Square Puzzle, often called the Sam Loyd 15-Puzzle, is a popular puzzle with sliding tiles, invented in the late 1800s. The usual version consists of a square enclosure with 15 square tiles, numbered from 1 to 15. They are arranged in a 4×4 grid, leaving one square in the grid empty. A move in this puzzle involves sliding any one of the tiles next to the empty square into the empty square. The objective of the puzzle is to start with a scrambled state and make the right moves to produce an ordered state with the tiles in row major order, as shown in the figure on the right.
In this part of the problem set we are going consider a generalized version of the fifteen puzzle with a n×n grid and n2 − 1 tiles. We will design a data structure for representing the state of the puzzle and write a solver that computes the moves to solve a given puzzle state.
Interface specifications. Design an interface for the data structure
that will represent the puzzle state. Think of clear and concise specifications
for the members of the interface. The file puzzle.mli contains an
incomplete signature PUZZLE to implement this interface. This
should help you start this task. You need to complete the signature by
filling in missing details and possibly correcting existing ones.
module type PUZZLE = sig
(* A puzzle is a configuration of a Sam Loyd 15-puzzle (size 4x4)
* generalized to size n×n for some n. *)
type puzzle
(* create n is a solved puzzle of size n×n. *)
val create
val of_list: int -> int list -> puzzle
val size
val do_random_move: puzzle -> puzzle
val fold_successors: ('a->puzzle->'a) -> 'a -> puzzle -> 'a
(* Print a puzzle. *)
(* Compare two puzzles *)
end
Representation. Choose an appropriate representation for the puzzle
state. Note that the representation should yield efficient (both in terms of
time and memory) implementations of the functions in the interface, thereby
helping in implementing an efficient solver. Based on this choice, define a
type puzzle in the Puzzle module:
module Puzzle : PUZZLE = struct
type puzzle = ...
...
end
Abstraction Function and Representation Invariant. Next to the definition of puzzle
include the abstraction function and representation invariant for your chosen representation
within comments
(* AF: ... *)
(* RI: ... *)
Basic Operations. Implement a function create n that takes in integer n
as argument and returns a solved puzzle of size n x n. Implement function of_list n tiles
to return a puzzle of size n and with tiles from the list tiles.
Implement function
fold_successors f init p that folds over the successor configurations reachable from
p using function f and initial value init.
Additional Operations. Implement additional operations from the signature. Function size p
returns the size of puzzle p. Function do_random_move p makes a random move
on puzzle p. This can be used in succession to create a scrambled state from the ordered one.
Also write a function to compare two puzzles, imposing a total ordering between puzzle states. This
may be useful in keeping track of puzzle states that have been seen so far during searching.
Implement a function to pretty-print the puzzle, to help debug your code. You may want to add more
operations to this ADT to implement your solver. You are asked to justify any operations you add, just like
you are asked to justify any specification changes you make.
Solver. Implement the signature Solver
module type Solver = sig (* * solve p is (s,n) where n is the number of positions searched, * and s is either Some of a list of puzzle states representing a * sequence of moves that solves the puzzle p, or else None if * there is no way to solve the puzzle. *) val solve: Puzzle.puzzle -> ((Puzzle.puzzle list) option * int) end
Your implementation for the data structure for Solver is allowed to contain additional definitions
not in the signature. For instance, depending on your solution search strategy, you might want to keep track
of the puzzle configurations considered so far. The OCaml Set functor may be useful for this.
You are also required to include adequate specifications along with the definitions.
In designing your puzzle abstraction and your solver, make sure there is a useful abstraction barrier between the two modules. The solver shouldn't have to know very much about what a puzzle is; a puzzle should expose operations needed to implement the solver, and little more.
Your solver needs to be fast enough to find a solution for a 3×3 puzzle in a couple of seconds.
Submit your data structure as a file puzzle.ml and your solver as solver.ml.
Karma Problem. Design a faster solver with clever heuristics, that can solve any given state of the 4×4 puzzle (the original 15-puzzle) in less than 5 seconds. The team that can solve for the largest puzzle (an n×n puzzle with the highest value of n) within 60 seconds will be rewarded with additional bonus points.
A quadtree is a data structure that supports searching for objects located in a two-dimensional space. To avoid spending storage space on empty regions, quadtrees adaptively divide 2D space. Quadtrees are heavily used in graphics and simulation applications for tasks such as quickly finding all objects near a given location, and for detecting collisions between two objects.
There are many variations on quadtrees, specialized for different applications. For this problem set, we'll implement a variation in which a quadtree represents a rectangular region of space parameterized by x and y coordinates: all the space between x coordinates x0 and x1, and between y coordinates y0 and y1.
A leaf node contains some (possibly empty) set of objects. A non-leaf node has four children, each covering one quarter of the original space, as shown in this picture:
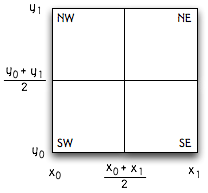
To find an object near coordinates (x,y), a quadtree is traversed starting from the top node and walking down through the appropriate sequence of child nodes that contain the point (x,y) until a leaf node is reached. The object or set of objects at the leaf can then be tested against. This figure depicts the quadtree nodes visited as the object at the black dot is searched for:

Document your implementation with a description of the abstraction function and of the representation invariant.
Implement and specify the quadtree data structure in quadtree.ml
It is up to you how you want to design and specify the quadtree, but be sure to read the tasks below carefully for they should give you a good idea of what sort of operations you might need. To get you started, you will probably want to write functions to make a new empty tree, add elements into the quadtree, efficiently query elements, and possibly fold over the tree.
Provide a function of the following signature which given a string representation of a file path, reads in a file of places and constructs a quadtree using this data. The function should use our provided parser function, and should return the populated quadtree.
val loadCityData: string -> quadtree
The main task to accomplish is to read in all the data provided in us-places.txt and efficiently implement the following function:
val citySearch: quadtree -> (float * float) -> (float * float) -> string list
Given a quadtree of city data, citySearch returns all cities lying
within specified ranges of latitude and longitude. For example,
citysearch qt (0.0, 5.0) (10.5, 20.5) returns a list of all the
cities between 0.0 and 5.0 degrees latitude and between 10.5 and 20.5 degrees
longitude.
Karma Problem. Additionally you may implement an alternative form of the citySearch function with the following signature:
val circleSearch: quadtree -> float -> (float * float) -> string list
Given a quadtree qt containing city data as above,
circleSearch qt r (lat,long) returns all cities within a distance
of r miles of the points at latitude lat, longitude
long. This is tricky to get right; one testing trick is to see
if you always match the answer returned by a reference implementation that is
brute-force, obviously correct, and likely much slower.
We have provided a parser for city data. The function parseFile takes in a string
representing a filename and parses it, returning a (float*float*string) list.
val parseFile : string -> (float * float * string) list
You may create your own files for testing purposes, but they must be formatted like the supplied file us-places.txt. Each line must have this format:
x-coord[SPACE]y-coord[TAB]name of location[NEWLINE (or end of file)]
Here, [SPACE], [TAB], and [NEWLINE] represent ASCII characters 32, 9, and 10 respectively.
Submit a file quadtree.ml which implements your data structure, and a file citySearch.ml which implements the loadCityData function, the citySearch function and optionally the circleSearch function. The fastest correct quadtree implementation will be granted bonus points. We will measure the speed of your (rectangular) city search.