Mathematical Interpretation of Fractal Dimension

The concept of "fractal dimension" is attributed to a 20th century mathematician, Benoit Mandelbrot. His fractal theory was developed in order to try to more precisely quantify the immense complexity of nature in relatively simple equations. His favorite example of such complexity was the craggy coast of Britain which, when seen from far above, looks somewhat wrinkled and convoluted. Yet as an observer gets closer and closer to the shore, the complexity of the coastline increases; smooth lines become jagged, and more jagged and complex until the observer is so close that he is observing the minute variation in the positions of each individual grain of sand along the shore. Moreover, we can imagine this observer measuring the length of the coastline with increasingly smaller rulers. As he takes account of the added complexity as he measures with increasingly precise resolution, his approximation to the length of the coast of Britain keeps increasing. In fact, he could very well find that the length he is looking for diverges to infinity!

Yet it is obvious that this "infinitely long" coast of Britain only encapsulates a finite area, just as a circle drawn on the globe can contain all of Britain. In some way, we believe that the coast of Britain is more "substantial" than a simple circle, and perhaps more interesting than a simple 1-dimensional line which defines a circle's circumference. Fractal dimension was developed as a way to quantify this contradictory complexity.

Explanation Image Exponent gives the dimension
Notice that a line segment is self-similar. It can be separated into 4 = 41 "miniature" pieces. Each is 1/4 the size of the original. Each looks exactly like the original figure when magnified by a factor of 4 (magnification or scaling factor). 4 = 41 pieces
The square can be separated in to miniature squares. If the smaller square is magnified (scaled)4 times then it is identical to the larger square. However, we need 16 = 42 pieces to make up the original square figure. 16 = 42 pieces
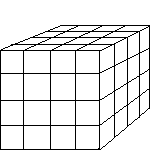
The cube can be separated into 64 = 43 pieces. Again, these pieces need to be enlarged (scaled) by a factor to 4 to generate the larger square. 64 = 43 pieces

Therefore, N (the number of miniature pieces in the final figure) is equal to S (the scaling factor) raised to the power D (dimension). In the previous cases it is easy to find the dimension by simply reading the exponent. This simple concept can be generalized to measure non-integral dimensions of many fractals. One such fractal is the Van-Koch snowflake which you generated in class. Another common fractal is the Sierpinsky Triangle discussed below, which is created by successively removing the middle section out of an equilateral triangle.

N = SD

 

This is a picture of a Sierpinsky Triangle: To generate it, we begin with an equilateral triangle. Draw the lines connecting the midpoints of the three sides and remove the center triangle. Note that our new triangle contains 3 "miniature" triangles. Each side = 1/2 the length of a side of the original triangle., and each "miniature" triangle looks exactly like the original triangle when magnified by a factor of 2 (magnification or scaling factor).


Now take the result and repeat (iterate) as shown.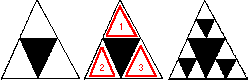

Continuing this pattern results in the figure above. The fractal is the limiting case that results when the iterations are continued out to infinity. Notice that the lower left portion of the triangle is exactly the same as the entire triangle when magnified by a factor of two, and the lower-left portion of that triangle is the same as it's containing triangle, and so on. The Sierpinsky Triangle is self-similar.

But what is the dimension of the Sierpinsky Triangle? Notice the second triangle is composed of 3 miniature triangles exactly like the original. The smaller triangles could be scaled by 2 to produce the entire triangle (S = 2). The resulting figures consists of 3 separate identical miniature pieces. (N = 3).

What is D? We simply take the logarithm of our above equation. Recalling than N = SD, 

SD       =     N
2D       =     3 
log(2D)  = log(3)
D*log(2) = log(3)
D        = log(3)/log(2)
D        = 1.585 (not an integer!)

In fact, a trivial computation from the above equation yields

D = log N/log S.

This is the formula to use for computing the fractal dimension of any strictly self-similar fractals. The dimension is a measure of how completely these fractals embed themselves into normal Euclidean space.

Identifying Dimension

For the following figures, we have given N, S, and D.

  1. Cantor Dust:
    N=2, S=3, D=log2/log3 =0.6309
  2. Box Fractal:
    N=5, S=3, D=log5/log3=1.4649
  3. Koch Curve
    N=4, S=3, D=log4/log3=1.2618
  4. Another one:
    N=8, S=4, D=log8/log4=1.5

Just for fun,
Find the dimension of fractals generated in each of the following ways:
(answers will be given in recitation sometime)

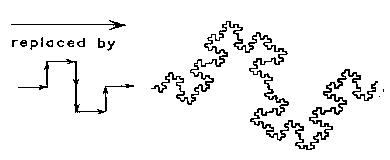
Initiator Generator
5.
6.
7.
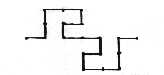8.
  1. Sierpinsky Carpet
  2. Menger Sponge

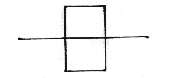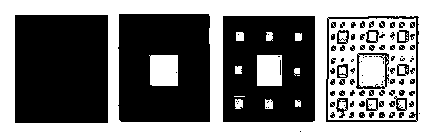
If you're interested in a more rigorous development of fractal theory, consult "The Fractal Geometry of Nature" by Benoit Mandelbrot. It is a seminal text in the field, and is written at an "educated layman's" level. For an even more rigorous discussion of more recent results, including computer applications, there are a few good good texts by Michael F. Barnsley, one of them is entitled "Fractals Everywhere" but it's pretty dense. Both of these books will have good bibliographies, too.

--Patrick White
All of the images above and some portion of text are borrowed from the PWS OnLine Series, Copyright © 1995 by PWS Publishing Company. I think my explication makes the concepts clearer, but this is based strongly on their web site.

Modified 1/29/98 by Alexey Nogin