CS1110 assignment A5

Assignment A5 CS1110 Fall 2010 Due 11:59pm Saturday, 30 October.

Purpose of assignment and basic ground rules

This purpose of this assignment is to

Introduce you to graphics
Give you practice with simple loops
Give you practice with recursion
Give you practice with helper methods and reusing previously written methods

Please read this entire document carefully. At the end of this document, we tell you what exactly to submit on the CMS. Budget your time wisely. Don't wait until the day before the deadline to do this assignment. We advise starting now and working on one or two functions a day. You may also want to experiment, drawing your own designs.

You may work with one other person. If you do so, FORM YOUR GROUP ON THE CMS WELL BEFORE YOU SUBMIT YOUR FILES. Remember, partners must work together and not independently.

Keep track of the time you spend on this assignment. You will be asked to put it in a comment at the top of file A5.java.

You need not use a JUnit testing class. You will (mostly) be looking at visual output (graphics) to determine correctnesss.

To save you time, we give you complete specifications of most of the methods you write. Please study them carefully. Note how precise and thorough they are. You should aim for this quality of specification when you write your own specifications.

Note on DrJava. Please do this immediately: In DrJava, use menu item Edit->Preferences; click Interactions Pane; and make sure the Require variable type box is unchecked. This will allow you to use variables in the Interactions Pane without declaring them. Also, change the indent level to 4 (Preferences category Miscellaneous).

Academic integrity

Please do not violate the Cornell Code of Academic Integrity. For this assignment, you may, of course, talk in general terms about problems and issues. But to be in possession of someone else's code for this assignment, from a previous semester or this semester, on paper or in electronic form, or to give someone else in the class your code is a violation of the code. It is stupid to copy because you don't learn anything, which is the main reason for the assignment. Moreover, forcing us to grade something that is not your own wastes our time.

This assignment is similar to one given in the past several semesters. Anyone caught using files that are obviously from a previous semester will be prosecuted, with the end result perhaps being to fail the course.

Directions

Download file A5.zip, unzip it, and put everything in it into a new directory. It contains:

1. File A5.java

2. File HSV.class, a simple implementation of the hue-saturation-value model (discussed later).

2. Package acm. It contains a directory of other packages, each of which contains a directory of .class files. These are machine-language versions of .java files. Do NOT load them into DrJava. The only thing you should load into DrJava is file A5.java. It will automatically use the .class files.

3. A directory doc, which contains specifications of all the classes in package acm. You will use these specs when writing method calls to draw things on the "graphics canvas". Outside of DrJava, double-click doc/index.html (or open it in a browser) to see the specs. Before you do any programming in DrJava, spend some time looking at the methods that you can use in classes GraphicsProgram, GTurtle, and GPen.

Package acm was developed under the auspices of the ACM (Association for Computing Machinery), the major CS professional society. Class A5 is a subclass of abstract class GraphicsProgram, which is part of the acm package. A GraphicsProgram is associated with a window on your monitor (much like class JFrame) that contains a "canvas" on which one can draw. When an instance of A5 is created, the associated window appears on your monitor. You can then create "turtles" and "pens" to draw (on the canvas) in that window.

An instance of class acm.graphics.GTurtle maintains a pen of a certain color at a pixel (x, y) that is pointing in some direction given by an angle (0 degrees is to the right, or east; 90 degrees, north; 180 degrees, west; and 270 degrees, south). When the turtle is moved to another spot using procedure forward, a line is drawn if its pen is currently "down" and nothing is drawn if its pen is "up". The pen is initially black, but its color, of class java.awt.Color, can be changed. A footnote on page 1.5 of the ProgramLive CD contains information about class Color.

By following the directions above, you've already looked at doc/index.html and studied the specifications of methods in class GTurtle as given in the javadoc files. Here are some important points:

Before an instance of GTurtle can be used to draw something, it has to be added to an A5 object. You can add many turtles to the same A5 object and draw different things with each. Function x.getTurtle(), which is already written, creates a new turtle and adds it to the instance of A5 whose name is stored in x. Read the function body carefully; make sure you understand what it is doing and how.
The coordinates and angle of the turtle are maintained using type double. This is needed for maximum accuracy. If ints were used, errors might crop up after many calculations. However, whenever a point is to be placed in the window, its x- and y-coordinates are rounded to the nearest integer because the graphics space works with ints.
Suppose t contains a GTurtle. The call t.forward(d) moves t d pixels in its current direction, t.setLocation(x,y) moves t to pixel (x,y) without drawing anything, t.left(a) turns t a degrees counterclockwise, and t.setDirection(a) sets its direction to angle a.
A turtle t moves with a certain speed, which must be in the range 0 <= speed <= 1, where 0 is the slowest and 1 the fastest. Not much detail on the speed is given, so we can't tell you more than that. Set t's speed to s using t.setSpeed(s);.

Notes

(1) t.setDirection(angle) does not redraw the turtle. For example, in the Interactions pane, try typing "a= new A5(); t= a.getTurtle(); t.setDirection(90);". The GTurtle obstinately continues to face west until you resize the window, and then it turns north.

(2) The zip file includes the "student view" ACM javadoc, which omits some information. If you are curious, you can view the complete documentation here.

Class A5 contains procedure drawTwoLines(s) to show you how graphics work. Compile class A5. Then, in DrJava's Interactions pane, create an instance of class A5 using a= new A5(); . The window with the canvas will appear. Execute the call a.drawTwoLines(0);. It should cause two lines to be drawn, waiting a few seconds before drawing each line. Study the body of drawTwoLines carefully, so that you know what each statement does.

In the Interactions pane (or in a method in class A5), draw some lines and rectangles to familiarize yourself with class Turtle. After that, perform the tasks given below. As you write a method body, refer constantly to the method specification and follow it carefully and rigidly. If you have to call another method, look at its specification and make sure you follow it. A huge number of programming errors arise from not following specifications carefully.

Task 1. Complete function toString(GTurtle) in A5. Follow the instructions given in the function itself. Here are two examples of what our toString function produces, and yours should be the same:

"GTurtle[location=(250.0, 250.0), color=GREEN, direction=270.0]"
"GTurtle[location=(250.0, 250.0), color=0x10203, direction=180.0]"

Your output has to be in this format —see the instructions given as a comment in A5.java's toString method.

Task 2. Complete procedure drawTriangle(GTurtle, int, Color). Then follow the instructions in the comment in the body to learn about rounding errors when using type double and why they don't really matter here. Note that the comment asks you to put some information at the top of file A5.java (as a comment).

Task 3. Complete procedure drawHex to draw a hexagon, as shown to the right of this paragraph, except the one to the right is green. It should call procedure drawTriangle 6 times. Some lines will be drawn twice, but that is OK. Follow the specification and hints carefully.

Task 4. Do TWO (repeat, 2) of 4A, 4B, or 4C. After you have completed the assignment, if you are interested, do the remaining one! It is fun to see how easy it is to do these neat things.

Note that each of these tasks involves creating a helper function with the same name (but different sets of parameters). Often, one makes helper functions private, as we've done here. The public function should call the private one. The user calls the public one, which does not take a GTurtle as argument, thus saving the user from having to know how to create a GTurtle.

The images shown below are only examples of what can be done. They are not precisely what you are expected to produce. You must follow carefully the specifications of the methods you will write

Task 4A: Draw a spiral. The first picture to the right is done by drawing 10 lines. The first line has length 5; the second, 10; the third, 15, etc. After each line, 90 degrees is added to the angle. The second diagram to the right shows a similar spiral but with 75 degrees added to the angle after each line. Ones that you draw will be similar, except that the first (small) line will be drawn to the east instead of the west.

Complete the TWO procedures named drawSpiral. The public one should call the private one. When you first test them, use 10 for d and 0 for s. Try different angles, like 90 degrees, 92 degrees, 88 degrees, etc. Use s = 0, or s = .5 to see the lines drawn one at a time.

You will be amazed at what these methods do. Find out by trying these calls, assuming that a is an instance of A5:

a.drawSpiral(.8, 1, 90, 300); a.drawSpiral(.85, 1, 135, 400); a.drawSpiral(.95, 1, 60, 100);
a.drawSpiral(.9, 1, 121, 300); a.drawSpiral(1, 1, 89, 400); a.drawSpiral(1, 1, 150, 300);
a.drawSpiral(.99, 1, 121, 500); a.drawSpiral(1, 1, 119, 500);

Task 4B: Draw many polygons. The first image to the right is a 20-sided polygon. The second image to the right is a series of 90 5-sided polygons of side length 50, the first started at angle 270, the second started at angle 274, the third at angle 278, and so on.

Complete the TWO multiPolygons procedures so that your program can draw such designs. The public one should call the private one. You can use procedure drawPolygon, which we give you. When finished, experiment to see what neat designs come out. Try, for example, a.multiPolygons(.8, 4, 100) and a.multiPolygons(.88, 30, 15).

Task 4C: Draw radiating lines. The picture to the right is done by drawing 15 lines of the same length, radiating out from the current turtle position. The angle between the lines is the same. If n lines are drawn, the angle between them is 360.0/n. The color of each line depends on the angle (the direction) of each line. To understand this, we explain two color models used on computers.

You probably know about the RGB color model (see the picture to the right): each color is represented by a certain amount of Red, Green, and Blue. RGB has its roots in the 1953 RCA color-TV standards and in the Polaroid camera. RGB is used in your TV and computer monitors, and hence on web pages. In the RGB model, the amount of each of red (R), green (G) and blue (B) is represented by a number in the range 0..255. Black, being the absence of the three main colors, is [0, 0, 0]; white, being the maximum presence of all three, is [255, 255, 255]. There are 16,777,216 different colors. Class java.awt.Color has some constants that you can use for some of the possible colors. For example, Color.magenta is [255, 0 , 255] (in the RGB model) and Color.orange is [255, 200, 0]. Web page http://en.wikipedia.org/wiki/List_of_colors gives (non-Java) names to many colors in the RGB model.

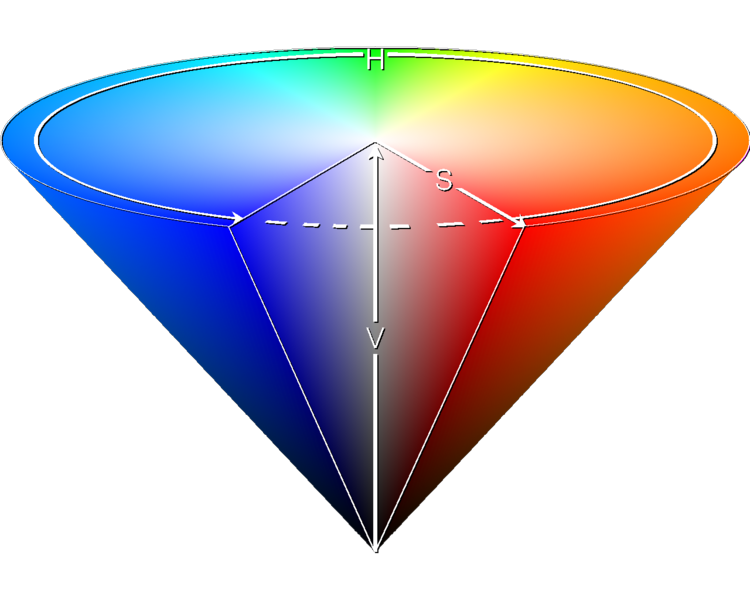Artists prefer the HSV (Hue-Saturation-Value) model over others because of its similarities to the way humans perceive color. HSV can be explained in terms of the cone that appears to the right.

H, the Hue, defines the basic color. H is an angle in the range 0 ≤ H< 360, if one views the top of the cone as a disk. Red is at angle 0. As the angle increases, the hue changes to orange, yellow, green, light blue, dark blue, violet, and back to red. The image in this paragraph shows the angles for some colors.

The Saturation S, in the range 0 ≤ S ≤ 1, indicates the distance from the center of the disk. The lower the S value, the more faded and grayer the color. The higher the S value, the stronger and more vibrant the color. The Value, V, in the range 0 ≤ V ≤ 1, indicates the distance along the line from the point of the cone to the disk at the top. If V is 0, the color is black; if 1, the color is as bright as possible.

Back to our radiating lines. Each line is drawn in the HSV color (hue, 1, 1), where the hue given by the angle at which it is drawn. But that HSV value has to be translated to the RGB system, because RGB is used by the turtle graphics system. So, we give you HSV.class, which allows you to create an object of the class and also contains a function that will translate an HSV value to the RGB system. See the note in procedure A5.radiate.

Complete the two radiate procedures. The public one should call the private one. As you write them, test them with small values of n, like 4 or 8. After the procedure is completely tested, try it with 360 lines of length 200, with turtle speed .85. Isn't that neat? Also, do it with 3,000 lines and turtle speed 1; notice how much more filled in the disk becomes.

Task 5. Recursive graphics. We now ask you to develop recursive procedures to draw some graphics, recursively. Do two of them: Sierpinski triangle , the Grisly snowflake, and the H-tree (but if you like this stuff, do all three!)

A GTurtle maintains a position and a direction, and when you ask it to draw using forward(d), it draws a line of length d in that direction. A GPen (also in package acm.graphics) maintains a position but no direction. Use procedure drawLine(dx,dy) to draw a line of length(dx,dy) from the pen's current position, ending up at the end of the drawn line, move(dx, dy) to do the same thing but without drawing, and setLocation(x, y) to move to position (x, y) without drawing. A GPen has other useful methods. Spend 5 minutes looking through their specifications.

We use a GPen instead of a GTurtle in task 5 because (1) there is no need to maintain the direction and (2) the GPen methods can be used to draw regions that are filled in with a color.

Again, for each of these recursive tasks, write two procedures: the private one that does the work and the public one that initializes the canvas appropriatly and then calls the private one to do the work.

1. Sierpinski triangles. Directly to the right is a filled-in equilateral triangle. We call it a Sierpinski triangle of size s (the length of a side) and depth 0. Next to it is a Sierpinski triangle of size s and depth 1. It is created by filling in 3 Sierpinski triangles of size s/2.0 and depth 0, in each of the corners of what would be a Sierpinski triangle of size s and depth 0. All the way on the right is a Sierpinski triangle of size s and depth 2; it is created by drawing 3 Sierpinski triangles of size s/2.0 and depth 1. In the same way, draw a Sierpinski triangle of size s and depth d by drawing three Sierpinski triangles of size s/2.0 and depth d-1 in appropriate places.

We have stubbed in two sierpinski procedures for you to complete. You can use procedure fillTriangle to draw a triangle —it is needed only at depth 0.

The most difficult part may be finding the height of the triangle with side length s. Knowing that it is an equilateral triangle, use the Pythagorean theorem to figure this out. Using h for the height, you should be able to visualize a triangle that is 1/2 of the equilateral triangle, with side lengths s, s/2.0, and h. Solve the formula s**2 = (s/2)**2 + h**2 for h.

2. Grisly snowflakes . To the right are three Grisly snowflakes of depth 0, 1, and 2. The depth 0 snowflake is simply a filled-in hexagon. The depth 1 snowflake of side length s is the depth 0 snowflake of side length s replaced by 7 hexagons of side length s/3.

In general, for d > 0, the Grisly snowflake of side length s and depth d consists of 7 Grisly snowflakes of side length s/3 and depth d-1, drawn at the obvious places.

As with Sierpinski triangles, the difficulty will be figuring out where each of the 7 Grisly snowflakes of depth d-1 go. We leave you to try to figure it out but will put some explanation later on on the course website.

We have stubbed in two grislySnowflake procedures for you to complete. The first, public one should set things up and then call the second one, which is private. We have also written procedure fillHex for you.

3. H-trees. To the right are three H-trees of size s and depths 0, 1, and 2. Here's how you draw them:

(1) Draw an H, with all three lines being of length s.

(2) If d>0, draw four H-trees of size s/2 and depth d-1. The centers of the four H-trees are at the top and bottom of the two vertical lines drawn in step (1).

H-trees are useful in designing microprocessor chips. The lines are wires that connect circuit components in a tree of interconnections, without wires crossing.

We have stubbed in two recursiveH procedures for you to complete. The first, the public one, should set things up and then call the second, private one.

We have also stubbed in procedure drawH, which may be useful to you. Complete it if you want to use it. For a pen p, draw lines drawn using procedures p.setLocation (to move the pen) and p.drawLine (to actually draw the line).

What to submit. Put a comment at the top of your A5.java that contains the following information.

Your name(s) and netid(s);
The information requested in Task 2;
The names of your two public recursive procedures;
What you liked best about this assignment;
What you most think could use improvement in this assignment; and
The time you spent on this assignment.

Make sure class A5 is indented properly and that all parts of the program can be seen without horizontal scrolling. Remove any System.out.println commands you may have put in for debugging purposes. Submit file A5.java on the CMS.