Ron Elber and Computational Molecular Biology

Ron Elber's research area is Computational Molecular Biology, with a focus on Structural Biology. He designs and applies algorithms to predict protein structures, to understand their dynamics and to investigate their function. He further explores interactions of proteins and their biological environment, for example, protein-membrane interactions. Structures of proteins are critical to the understanding their function. Experimentation is slow in producing the desired structures and is not always successful. Therefore, considerable effort is focused on developing computational approaches for structure prediction.

Structure determination

1. Coupled optimization of structures of homologous proteins. Elber explores the empirical observation that homologous proteins (proteins of the same family) fold to similar structures and combines this observation with global optimization of an energy function. Significant improvement (compared to the use of energy function only) was demonstrated for structure prediction of protein families (pancreatic hormones - ppt, and DNA binding proteins - homeodomains) [1]. The averaging of sequences (on different members of the family) and the averaging of alternate transient conformations provides a new minimum with a significantly larger radius of attraction [2].

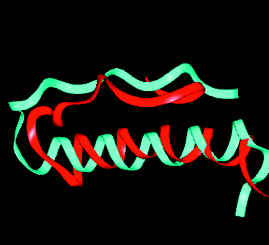Structure prediction of pancreatic hormone.  Blue - native structure.  Red - predicted structure.

2. Design of folding potentials. One of the prime difficulties of the protein folding problem is the lack of proper potential energies (or scoring functions). A minimal requirement is that the energy of the native structure will be lower than the energies of all other possible conformations. Of course, other conditions might be added, such as a smooth energy surface, which is more accessible to global optimization. However, even the minimal request stated above is not satisfied by any known energy function. He has formulated a set of linear inequalities and decoy structures to obtain potential parameters that satisfy the above criterion for a set of conformations. One useful feature of the above formalism is the ability to prove that some models could not possibly work, making it possible to propose essential modifications of the scoring function.

Even if the structure is known, questions may be left unanswered and new puzzles may appear. For example, the biologically active structure of the protein can be a rare fluctuation that is not observed in the average experimental structure. These fluctuations can be studied with the method of Molecular Dynamics. Elber develops theoretical approaches and algorithms to extend the scope of the Molecular Dynamics method and applies them to a variety of biophysical problems.

Protein dynamics

1. Mechanisms and dynamics of peptide folding. Peptides are short polymers of amino acids. They serve as model systems for nucleation sites in protein folding. It is believed that protein folding proceeds via a time sequence of nuclei of structures. The identity and the physical forces that hold the initiators of structure are a topic of intense investigations by theorists and experimentalists. He performed atomically detailed simulations of peptide folding [3] using a novel algorithm for global optimization of structure. The results indicate that long-range electrostatic attraction and the local propensity of the proline are the prime initiators of the folding process.

2. Algorithms for long time dynamics. The usual approach of Molecular Dynamics is limited to time scales of a few nanoseconds, far shorter than the time scales of many biophysical processes. Elber developed a new technique to compute approximate molecular dynamic trajectories at very extended time scales. The method is based on a stochastic difference equation that models numerical errors. Elber has formulated the theory, provided numerous examples for Newtonian mechanics [4], and further exploited properties of Brownian trajectories [5]. He is employing the new methodology to investigate ion channels and conformational transitions in proteins.

References

[1] Simultaneous and coupled energy optimization of homologous proteins: A new tool for structure prediction. Folding and Design 2 (1997), 247-259 (with C. Keasar and J. Skolnick).

[2] Homology as a tool in optimization problems: Structure determination of 2D hetero-ploymers. J. Phys. Chem. 99 (1995), 11550 (with C. Keasar).

[3] Kinetics of peptide folding: Computer simulations of SYPFDV and peptide variants in water. J. Mol. Biol. 272 (1997), 423-442 (with D. Mohanty, D. Thirumalai, D. Beglov, and B. Roux).

[4] Calculation of classical trajectories with a very large time step: Formalism and numerical examples. J. Chem. Phys. 105 (1996), 9299-9315 (with R. Olender).

[5] Yet another look at the steepest descent path. J. Mol. Struct. Theochem and Proc. WATOC Symp. (1997), 398-399,63-72. (with R. Olender).