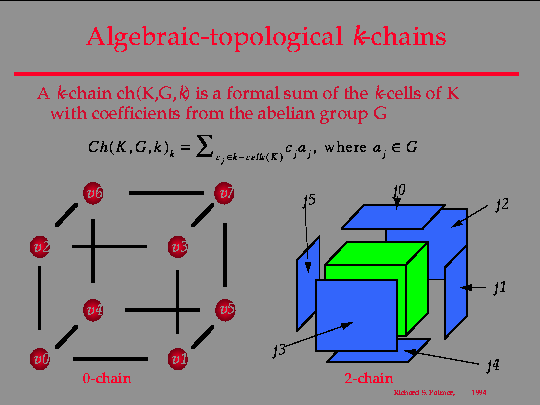
So at this point we have seen how a cell complex can be used to partition a complex system into a set of simpler systems, each of which is represented by a cell. An algebraic-topological k-chain is a means of associating state with the k-cells of a complex. Formally, three things are needed to define a k-chain: a complex K, an abelian group G, and an integer k. You may recall that a group is a set S, together with an operation, denoted +, that maps pairs of elements (a, b) in S to a third element c in S (a, b and c not necessarily distinct) a distinguished element called the identity (denoted 0), such that every element has an inverse, i. e. , if a in S then there is b in S such that a + b = 0. An abelian group is a group with a commutative operation +. That is, for all a and b in S, a + b = b + a. We will see why the definition of chain requires an abelian group when we consider the operations boundary and coboundary. Often we will assume that G is the set of real numbers under addition. (This satisfies the conditions for an abelian group. ) In this case, we may view a k-chain as an assignment of a real number to every k-cell in the complex. Other times, the abelian group could be the set of polynomials defined over a set of variables. The operation in this case is the addition of polynomials. This is illustrated in the slide. On the left is an illustration of a 0-chain -- as assignment of a variable to each 0-cell. If we assign a value to each variable (for instance, elements of the vector space R^3), we have a means of embedding the 0-cells of K in space. On the right we see an example of a 2-chain defined over the same complex K. In this case we have assigned a variable to each of the 2-cells in the complex. Similar to the case with the 0-chain, we might have instead assigned real numbers to the 2-cells. This might be done, for instance, to represent some physical phenomenon associated with a 2 two dimensional region of space. The ability to define both abstract (e. g. , polynomial valued) and concrete (e. g. , real valued) chains over a cell complex is important because it provides a means of moving from an abstract definition that applies to a wide range of situations(e. g. , abstract, unembedded complexes) to a particular mathematical model for a given instance -- the definition may be parameterized by its embedding.