User-specified functions in QMG

The size-control function is a string. A simple example of a legal size-control string is (const 0.1); this denotes the function that returns the constant value 0.1 (i.e., the desired mesh size is 0.1). There are three places where this size-control string can be specified.

First, it can be attached as a property-value pair to a face of a brep. In this case, the property name is sizecontrol, and the value would be the string (const 0.1). A size-control function attached to a face acts only on the part of the mesh near that face. The routine to add property-value pairs, including sizecontrol, is gm_addpropval.

The second place this string is specified is as a keyword argument to gmmeshgen. The keyword name is sizecontrol Thus, the user can say (in Matlab)

m = gmmeshgen(b, 'size', '(const 0.1)');

The third place a size-control string is specified is in gmmeshgen.m or gmmeshgen.tcl; in these files the default size control is defined to be (const 1e307).

If multiple size control parameters are specified, then all of them act as upper bounds.

Here is an example of using const size control functions. Suppose the user types in Matlab:

t = gm_cpoly([1,1; 0,2; -1,1; 0,-3], [0;3;1;1]);
t{6}{1,2}={'sizecontrol'; '(const 0.05)'};
m = gmmeshgen(t, 'sizecontrol', '(const 0.3)');


gmset t [gm_cpoly {{1 1} {0 2} {-1 1} {0 -3}} {0 3 1 1}]
gmset t [gm_addpropval $t e4 {sizecontrol} {"(const 0.05)"}]
gmset m [gmmeshgen $t size "(const 0.3)"]


The first line creates a brep shaped like the outline of an ice-cream cone. The second line attaches a size control property to one edge of the cone (the edge whose facespec is 1:2) that requests triangles of size 0.05 or smaller. The default size passed into the mesh generator is size 0.3. Therefore, the mesh generator will generate triangles with side lengths approximately 0.3, except in the neighborhood of the specified edge, where they will be size approximately 0.05. In between the two regions the mesh size will decrease smoothly. Here is how the mesh appears:

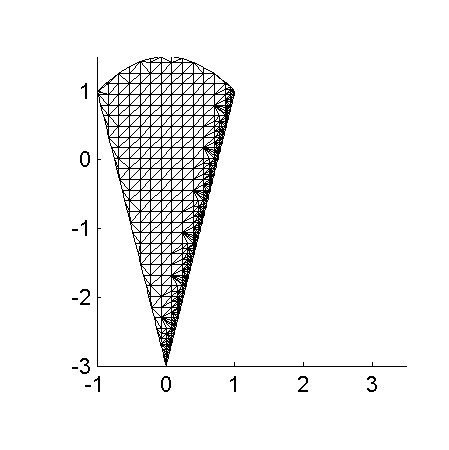
Note that the size control parameter acts as an upper bound, but the actual mesh size could be smaller. This is because the mesh generator must take into account geometric constraints imposed by the domain itself. For instance, in the above ice-cream cone example, if we had specified "(const 20)" as the size control argument, clearly we should not expect triangles of side-length 20 as output.

Another valid size control function is an string containing a formula. In this case, the function has the form (formula expression). The expression is a usual arithmetic expression containing numbers, +, -, *, / , (), and so on. Special functions like sqrt, log, and so on are also OK. In addition, the expression can contain the special symbols %0, %1, and %2 which represent the coordinates of the point at which the size control function is being evaluated (the first coordinate is %0, the second is %1, and so on).

Here is an example of this. Suppose you type in Matlab:

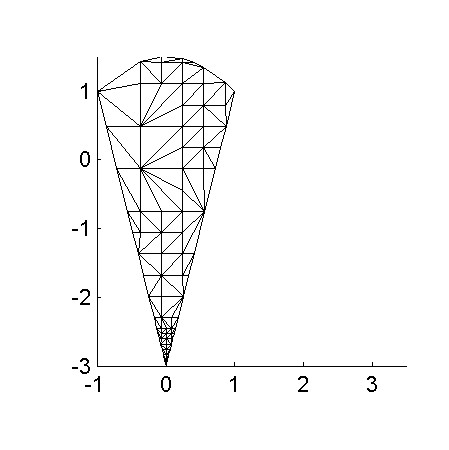
t = gm_cpoly([1,1; 0,2; -1,1; 0,-3], [0;3;1;1]);
m = gmmeshgen(t, 'sizecontrol', '(formula abs(-3.02-%1))');


The expression is evaluated either by the Tcl expr function or the Matlab eval function. These two functions have fairly similar expression syntax; the above example works the same in both expression evaluators. One important difference is exponentiation. In Tcl you say pow(a,b) whereas in Matlab you say a^b. A second important difference is that Tcl switches to integer arithmetic if it detects all integers in an expression, in contrast to Matlab, which always uses floating-point arithmetic. Thus, you should avoid something like "%0/10" in a Tcl expression because if %0 happens to be 1, then this expression would evaluate to 0. Instead you should say "%0/10.0".

Security note: the Matlab eval function has the ability to execute arbitrary shell commands. Therefore, if you receive a brep from an untrusted source, check the property/value pairs carefully for undesirable shell commands. In Tcl, the expression interpreter is made safe using a call to Tcl_MakeSafe, which gives an added measure of security against arbitrary shell commands.

In both Matlab and Tcl, the size control string is processed by functions called gm_sizecontrol and gm_sizecontrol_interior. The former is used for points on the boundary, and the latter for points on the interior. In Tcl, these functions are located in file qmg_sizecontrol.tcl. These functions make sure that the size control string is a parenthesized list and that the first item in the list is either const or formula. Then they substitute actual point coordinates for %0, etc., if the size control is a formula and compute the value. These functions gm_sizecontrol and gm_sizecontrol_interior are invoked by a C++ routine in source file sizectl_fe.cpp of the mesh generator. There are two versions of this source file, one for Matlab and one for Tcl.

The size control scheme is reasonably general, but the user might want to customize it further to suit his/her own needs, for instance, by tying the size control to a posteriori error indicators. In this case the user should rewrite gm_sizecontrol. There is an additional hook to help with customization of the size control. The keyword option userdata can be passed to the mesh generator (e.g., m = gmmeshgen(t, 'userdata', 'somestring',...)); the value of this string is passed verbatim to gm_sizecontrol and gm_sizecontrol_interior on every invocation as one of their arguments. Neither routine uses this argument.

Another user-specified function for the mesh generator is the curvature control. This is specified by a value attached to property curvecontrol associated with faces. It is also specified by a curvecontrol keyword option to gmmeshgen. This function is interpreted by function gm_curvecontrol in both Matlab and Tcl. In Tcl, this function is located in file qmg_sizecontrol.tcl.

The other functions specified by the user—conductivity, source term, and boundary conditions—are all associated with gmfem (Matlab only). The specification of these is very similar, except there is an alternate form of specifying a formula: vecformula. If the user specifies a vecformula, then when the formula is eval'd, %0 will have substituted a column vector of x-coordinates instead of a single x-coordinate, and similarly for %1 and so on. (The column vector for %0 will have the same number of entries as the vector for %1). The formula is expected to return a column vector of function values of the same size. The purpose of the vecformula option is to speed up processing in Matlab, since vector formulas are much faster than evaluation by loops. An example of a vector formula would be (vecformula (sqrt(%0.^2 + %1.^2))).

Conductivity is handled by gm_conductivity, which can be customized by the user as mentioned above. The default conductivity is (const 1.0). As above, the user can specify conductivities as property-value pairs to top level faces only or as an argument to gmfem. The property name for conductivity is conductivity. If the user specifies both, then the property-value pair takes precedence.

Source terms are handled by gm_source. The default is (const 0.0). Source terms can also be property-value pairs of top level faces. As with conductivity, property value pairs take precedence over specification as an argument to gmfem. The property name for a source term is source.

Boundary conditions are handled by gm_bdrycond. Unlike conductivity and source, there is no argument to gmfem for boundary conditions; they must be property-value pairs on the faces of the brep of dimension d−1, where d is the dimension of the brep. The property name is bc. The value is the boundary condition, which has a somewhat different syntax. It is specified as an ordered pair (type string); where type is either d or n (for Dirichlet or Neumann) and string is a string of the kind described above, for example, (const 0.1) or (formula %0+%1). The parentheses are part of the syntax. The default boundary condition is (n (const 0)), i.e., du/dn=0, which corresponds to an insulated boundary. Thus, for a 2-dimensional problem, to add a Dirichlet condition of constant 10.0 to face 1:2, you would type

[scrap,p] = size(t{6}{1,2});
t{6}{1,2}{0,p}='bc';
t{6}{1,2}{1,p}='(d (const 10.0))';


This documentation is written by Stephen A. Vavasis and is copyright ©1999 by Cornell University. Permission to reproduce this documentation is granted provided this notice remains attached. There is no warranty of any kind on this software or its documentation. See the accompanying file 'copyright' for a full statement of the copyright.