

The categories of functionality are:
If an argument or return variable is a brep or simplicial complex, then the argument/return variable is in chunk format unless otherwise indicated.
After the name of each routine, there is an indication whether it is written Matlab, Tcl/Tk, or C++. For routines written in C++, we indicate the Matlab and Tcl/Tk calling formats.
Arguments in curly braces are optional. The text describes the default values for optional arguments. Many of the routines take an optional 'tol' argument as their last argument. There is a separate page about the tol argument.
Other standard formats for arguments are as follows. Vectors and matrices in Matlab are just ordinary vectors and matrices. Vectors in Tcl are lists, and matrices in Tcl nested lists. See the syntax synopsis for an example. String literals in Matlab must be quoted with single quotes. In Tcl/Tk double quotes are used for string literals, and are optional unless the string has embedded spaces.
gm_addpropval(a,1,0,'color','<1 1 1 1>');
does not anything by itself; in particular it does not modify
the brep a. In a future version of QMG, we may offer object-oriented
constructors.
At the C++ level, the underlying
functions like Qmg_Brep_Unpacked_1::add_face() are indeed
object oriented and are not call-by value.
Matlab:This function adds a new face to the given brep. The face is added at dimension dim. The new face will be the highest-numbered face of that dimension. Arguments eq is a matrix with orthonormal rows and rhs is the right-hand side vector. Together these two arguments specify the linear equations Ax=b containing the hull of the new face. Argument point is a vector containing a point in the relative interior of the new face.newbrep=gm_addface(brep, dim, eq, rhs, point);Tcl/Tk:
gmset newbrep [gm_addface $brep $dim $eq $rhs $point]
Note that if you want to build a brep, but you want QMG to figure out the affine coefficients, rhs and point, you can alternatively construct the brep as a string and then execute gm_in on the string. (You must specify the coordinates of 0-dimensional faces with this technique.) This is the technique used in gmcone.
The new face has no children, internal boundaries, or property-value pairs. These can be inserted with gm_addpropvl and gm_addsubface.
See the cautionary notes.
Matlab:This function adds a new property-value pair to a face of a brep, and returns the so-modified brep. Arguments fdim and faceind indicate the facespec of the face to modify. Arguments prop and val are both strings. If the property already exists, then this routine replaces its old value with val. The built-in properties (children, internalboundary, affine_coef, affine_rhs, point) cannot be changed with this function.newbrep=gm_addpropval(brep, fdim, faceind, prop, val);Tcl/Tk:
gmset newbrep [gm_addpropval $brep $fdim $faceind $prop $val]
To delete a property-value pair from a face, set the val to the empty string.
Property names of faces are not case sensitive.
See the cautionary notes.
Matlab:This function adds a subface (i.e., an internal boundary or a bounding child face) to a face of a brep. The input brep is the first argument. Arguments fdim and faceind are the facespec of the face that will get the subface. Argument type is 0 for an internal boundary and 1 for a child. Finally, arguments subfacedim and subfaceind are the facespec of the subface that is getting added.newbrep=gm_addsubface(brep, fdim, faceind, type, subfacedim, subfaceind);Tcl/Tk:
gmset newbrep [gm_addsubface $brep $fdim $faceind $type $subfacedim $subfaceind]
See the cautionary notes.
Matlab:This function creates an empty brep (no faces) whose embedded dimension is the given argument. Generally one starts adding faces to this object with gm_addface. The intrinsic dim is initially -1 and goes up as faces are added.newbrep = gm_emptybrep(dim);Tcl/Tk:
gmset newbrep [gm_emptybrep $dim]
Matlab:This routine creates a 2D polygon. The argument vtxlist is a matrix of vertices. Each row has two entries that are vertex coordinates. These are the vertices of the polygon in consecutive order. (It doesn't matter whether the order is clockwise or counterclockwise.) This list of vertices may be contain several different loops (if the boundary of the polygon has more than loop). The integer array startpos is an increasing array of integers; each of these integers is a row index into matrix vtxlist. Each entry in startpos is the starting position of a loop. Array startpos must have at least one entry: its first entry must be zero since the first loop starts at position 0.newbrep = gm_poly(vtxlist, startpos {, tol});Tcl/Tk:
gmset newbrep [gm_poly $vtxlist $startpos { $tol}]
A graphical front-end to this routine is provided by
gmmouse.
Matlab:This function deletes the face whose facespec specified by (fdim,faceind). It then renumbers the faces of that level, and updates the child and internal boundary lists of higher-dimensional faces for the new numbering. A warning is printed on the console if you delete a face that is referred to as a subface by a higher-dimensional face. (A brep with a dangling child/internal boundary index can cause a segmentation violation.)newbrep = gm_rmface(brep, fdim, faceind);Tcl/Tk:
gmset newbrep [gm_rmface $brep $fdim $faceind]
Matlab:This function creates a new simplicial complex whose intrinsic dimension is idim (integer), whose embedded dimension is edim (integer), with coordinates located at vtxcoord (matrix with real entries, one row per vertex), simplices specified by smpvtx (matrix with integer entries; each row is the indices of the vertices that define that particular simplex), and vertex sources specified by vtxsource (integer matrix with two entries per row; each row is a facespec). In smpvtx, the number of vertices starts at 0.newsmpcomp = gm_simpcomplex(idim, edim, vtxcoord, smpvtx, vtxsource);Tcl/Tk:
gmset newsmpcomp [gm_simpcomplex $idim $edim $vtxcoord $smpvtx $vtxsource]
Matlab:
[p,l,s,c]=gmbasics;
The four return variables are four breps, which are
the following: a point embedded in R^0,
a line segment embedded in R^1, a square embedded
in R^2 and a cube embedded in R^3. The segment is [0,1], the
square is [0,1] x [0,1] and the cube is [0,1] x [0,1] x [0,1].
The Tcl/Tk version is slightly different:
Tcl/Tk:
gmset b [gmbasic $dim]
where $dim is the dimension of the unit object that you want
(e.g., $dim=2 sets b to a square).
Matlab:This routine constructs a halfspace, that is, a set of the form {x: a'x<=b}. Argument nrml is the vector a in this formula, and scalar argument rhs is the scalar b in this formula.brep = gmhalfspace(nrml, rhs);Tcl/Tk:
gmset brep [gmhalfspace $nrml $rhs]
Matlab:This routine allows the user to click the mouse in the drawing window to draw the boundary a 2-D brep. The boundary is composed of one or more closed paths. A brep is returned. This function passes the sequence of clicks directly tobrep = gmmouse;orbrep = gmmouse(tol);Tcl/Tk:
gmset brep [gmmouse {$tol}]
gm_poly.
The paths may be clicked in either clockwise or counterclockwise order.
The user should not click a path in which boundary segments cross
through each other. The program does not currently check for
this error condition, but this can be checked with
gmcheckbrep.
Matlab:Here, k is an integer 3 or larger. This routine constructs a regular polygon (a 2D brep) with k sides centered at the origin. The polygon is scaled so that it is inscribed in the unit circle.brep = gmpolygon(k);Tcl/Tk:
gmset brep [gmpolygon $k]
gmapply function. A transformation matrix
is m-by-(n+1), with m>=n. The last column of a transformation is
a translation; the first m-by-n columns are a linear operator.
Matlab:Each arg is a nonzero real number. The result is a d-by-(d+1) transformation that does dilation of the coordinates. Negative entries do reflection. The number of arguments d can be as large as 6.mat = gmdilate(arg1,arg2,...,argd);Tcl/Tk:
gmset mat [gmdilate $arg1 $arg2 ... $argd];
Matlab:This routine constructs a d-dimensional rotation in plane coord1-coord2. The amount of the rotation is angle radians in the counterclockwise direction. If there is only one argument to this routine, then d=2 is assumed, and the plane rotation is in the (x_1,x_2) plane.mat = gmrotate(angle {, d, coord1, coord2});Tcl/Tk:
gmset mat [gmrotate $angle { $d $coord1 $coord2}]
Note that the third and fourth argument, coordinates, are numbered starting from 1 in Matlab but starting from 0 in Tcl/Tk.
Matlab:Each arg is a real number. This routine constructs a d-dimensional translation operator, where the translation amounts in each dimension are the arguments. The number of arguments can be as large as 6.mat = gmtranslate(arg1,arg2,...,argd);Tcl/Tk:
gmset mat [gmtranslate $arg1 arg2 ... $argd]
Matlab:Here, obj1 is a brep or simplicial complex, and mat is an affine transformation of the correct dimension. The affine transformation is applied to the object, and the transformed object is returned.obj2 = gmapply(mat, obj1{, tol});Tcl/Tk:
gmset obj2 [gmapply $mat $obj1 {$tol}]
This function, when applied to breps, assigns the same property-value lists to faces of the output brep that were assigned to the input brep.
The mat argument can be any matrix of
size m-by-(d+1), where d is the embedded dimension
of the object and m>=d. This matrix can be constructed
using some combination of transformation constructors,
possibly combined with gmcompose.
If we partition the matrix as [A,b] where
A is m-by-d and by is m-by-1, then the transformation applied
is x --> Ax-b.
Matlab:This routine applies the boundary operator to a simplicial complex, and returns the resulting simplicial complex. The resulting simplicial complex has the same embedded dimension, an intrinsic dimension of one less, and a subset of the vertices.newsimpcomp = gmboundary(simpcomp);or:
[newsimpcomp, vtxsrc] = gmboundary(simpcomp);Tcl/Tk:
gmset lst [gmboundary $simpcomp]
The second return argument vtxsrc is an array of integer indices. This array has one entry for each vertex of the new simplicial complex. This entry is the index of the corresponding vertex in the original simplicial complex.
In the Tcl/Tk version, the return variable is a list with two elements, the first being the new simplicial complex and the second being the integer array (vtxsrc).
Matlab:This routine simplifies a brep by repeatedly calling the C++ routine gm_brepsimp(brep,j,tol), with j=0,1,2. Each time it calls this routine, it checks whether the number of brep faces decreases or child and internal boundary links decreases. When the numbers stop decreasing, the routine returns the resulting brep.newbrep = gmbrepsimplify(brep {, tol});Tcl/Tk:
gmset newbrep [gmbrepsimplify $brep {$tol}]
The lower-level routine gm_brepsimp(brep,opcode,tol) simplifies a brep in one of three ways. If opcode is 0, it tries to merge faces of the brep with the same dimension and same affine hull. Merging can take place only if the two faces have the same collection of parent faces.
If opcode=1, then gm_brepsimp searches for faces containing interior boundaries that are external to the face. Such internal boundaries are then unlinked from the face containing them.
If opcode=2, gm_brepsimp deletes all internal boundaries that can be legally deleted. An internal boundary can be legally deleted only if it is a subface of a zero or one superfaces.
This routine can be called after the boolean operations to get rid of unwanted internal boundaries. For instance, suppose you execute:
[p,l,s,c]=gmbasics;
s2 = gmunite(s, gmapply(gmtranslate(1,0)), s);
In other words, you unite the unit square with a copy of the unit
square translated right by 1 unit. The result s2 will be a brep
that looks like this:
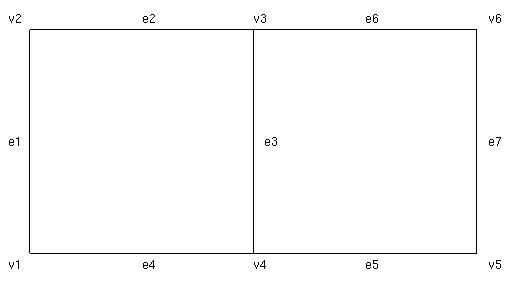
The gmbrepsimplify routine will first merge e2 and e6, as well as e4 and e5. It will also delete the internal boundary e3. Then it will notice that v3, v4 are internal boundaries of the new merged edges and delete them. The result will be a rectangle with four sides (two sides of length 2 and two of length 1) and four vertices.
Matlab:This routine splits the input object obj (either a brep or simplicial complex) into connected components. The return value depends on whether the object is a brep or simplicial complex. If it is a brep, then the return value is a new brep. In this new brep, every face has been individually split into connected components. Each face of the new brep assigned a property name "previous" whose value is the facespec of the face in the input brep of which it is a component. In addition, each face is tagged with a property-value pair "component" followed by an integer. This tag identifies which component of the whole brep contains the face. The components are numbered sequentially starting from 0.result=gmcompo(obj, {tol});Tcl/Tk
gmset result [gmcompo $obj {$tol}]
If a face has an internal boundary that is external to the face itself, then this internal boundary is dropped by gmcompo.
If the input argument obj is a simplicial complex, then the return variable is an integer array whose number of entries is equal to the number of vertices in the simplicial complex. These integers identify which component contains the specified vertex. The components are numbered sequentially starting from 0.
Matlab:If brep1 has embedded dimension d, this creates a new brep with embedded dimension d+1. The new brep is a cone whose base is a copy of brep1 embedded in the x_{d+1}=0 plane. The second argument is the apex of the cone. It must be a d+1-vector whose last entry is not zero.brep2=gmcone(brep1,point {, tol});Tcl/Tk:
gmset brep2 [gmcone $brep1 $point {$tol}]
The gmcone function ignores the property-value lists of faces of the input brep, and its output brep has no property-value pairs initially.
Matlab:Argument obj1 is either a brep or a simplicial complex. If the object has embedded dimension d, this creates a new object with embedded dimension d+1. The new object is simply a copy of the old one, embedded in the x_{d+1}=0 plane of the higher dimensional space.obj2=gmembed(obj1 {, tol});Tcl/Tk:
gmset obj2 [gmembed $obj1 {$tol}];
The gmembed function calls gmapply
with a matrix that consists of the identity with a row of zeros
concatenated (for the new dimension) and a column of zeros (for a
translation of zero) concatenated.
Matlab:If brep1 has embedded dimension d, this creates a new brep with embedded dimension d+1. The new brep is the prism formed by joining a copy of brep1 embedded in the x_{d+1}=0 plane to a parallel copy in the x_{d+1}=height plane. If the height argument is absent, the default value is 1.brep2=gmprism(brep1 {, height {, tol} });Tcl/Tk:
gmset brep2 [gmprism $brep1 { $height { $tol} }]
The gmprism function, like gmcone, clears property-value pairs.
Matlab:This routine computes either a complement or an outside/inside version of an object. If the opcode argument is 0, the routine computes a complement. The complement for a full-dimensional object is defined as follows. All boundary faces of lower dimension stay the same. The toplevel face is replace by a toplevel face consisting of those points that are not in any boundary and were not in any toplevel face of the input brep. (There may not be any such points, in which case the complement has no toplevel face.)brep2=gm_unary(brep1 , opcode {, tol} );Tcl/Tk:
gmset brep2 [gm_unary $brep1 $opcode { $tol}]
The complement of an object that is not full-dimensional is a new brep with all the same lower dimensional faces, and a toplevel face that is all of R^d, with internal boundaries that are the lower dimensional faces.
Note that the complement of the complement of g is not necessarily g. The complement of the complement differs in the case that g has multiple top-level faces ( g is said to be "MTL" in this case). In this case, the complement of the complement will have a single top-level face, and any subface that bounded two top-level subfaces of the original g will now be an internal boundary of the new g.
If the opcode is 1, the routine computes an inside/outside version of the object. This is an object has the same top-level face or faces as the input brep, plus one additional toplevel face that is the complement of all the original top-levels. Thus, the inside-outside version has top level faces covering all of R^d, where d is the embedded dimension of the brep.
gm_bool,
a C++ routine
that computes intersections. Function gm_bool may also
invoke the C++ routines underlying
gm_unary depending on the operation code given to it.
If A,B are two breps, then their intersection C is defined as follows. First, A and B must have the same embedded dimension. Consider embedding both of them in the space of their embedded dimension, say R^d. Label each point of R^d with the facespec of the lowest dimensional face of A containing the point, and also the lowest dimensional face of B. A point that is not in A or B is missing one of its labels. Only points that have both labels present are in the intersection. The faces of the intersection are defined by taking equivalence classes of points that have the same pair of labels.
If some of the faces of A or B have property-value pairs, then if this same face appears (either partly or in whole) in C, then its appearance in C is also marked with the same property-value pairs.
The algorithm for boolean operations is a fairly naive looping over all pairs of faces. The complexity of a boolean operation is O(mn(m+n)) where m is the combinatorial complexity of the first object and n is the combinatorial complexity of the second object. The standard reference for boolean operations on geometric objects is C. Hoffmann, ``Geometric and Solid Modeling: An Introduction,'' Morgan Kaufmann, 1989. The algorithms used in gm_bool for processing degeneracies (see below) are not the algorithms in Hoffmann's book, however. Optimizations to improve running time described in the book, such as face boxing, have not been implemented.
The result of set boolean operations often have internal boundaries because of degeneracies. Suppose that the embedded dimension is d, U is a face of A of dimension e, and V is a face of B of dimension f. Then in the generic case we would expect either that U and V do not meet or else that the intersection of U and V has intrinsic dimension e+f-d.
If the intrinsic dimension is some other integer, this is called a degeneracy. The set boolean routines check for degeneracies, and if so, carefully work around them in order to produce a correct brep. We believe that, in the presence of exact arithmetic, the set-boolean operations correctly handle degeneracies of any dimension. However, because the operations are implemented in double-precision floating point, there are cases when the degeneracy routines might fail. For instance
c = gmunite(a,gmapply(gmrotate(1e-12),a), 1e-13);
(that is, the union of a two-dimensional brep with a copy of it
rotated by 10^(-12) radians) will very likely cause the routine
gm_bool to generate an error or an erroneous brep.
Unwanted internal boundaries
can be deleted with
gmbrepsimplify.
Matlab:This function computes the geometric intersection of two breps. See the preceding notes for the details on what "intersection" means.newbrep=gmintersect(brep1, brep2 {, tol} );Tcl/Tk:
gmset newbrep [gmintersect $brep1 $brep2 { $tol}]
Matlab:This operation splits brep1 into two pieces, the part inside brep2 and the part outside brep2. The two pieces are both returned as the two top-level faces of newbrep. The resulting brep thus may have one or more MTL internal boundaries. This routine is equivalent to the intersection of brep1 with the outside/inside version of brep2. See the preceding notes for the details on what "intersection" means. See the notes on gm_unary for information about computing outside/inside breps.newbrep=gmsplit(brep1, brep2 {, tol} );Tcl/Tk:
gmset newbrep [gmsplit $brep1 $brep2 { $tol}]
Matlab:This computes the set difference brep1 minus brep2 is computed. This routine is implemented as the intersection of brep1 with the complement of brep2. See the preceding notes for the details on what "intersection" means. See the notes on gm_unary for information about computing complements.newbrep=gmsubtract(brep1, brep2 {, tol} );Tcl/Tk:
gmset newbrep [gmsubtract $brep1 $brep2 { $tol}]
In the case that brep2 has a lower dimension than brep1, this routine is a useful way to create SL internal boundaries.
Matlab:This operation computes the set union of two breps. The set union is defined to be the complement of the intersection of the complement of brep1 and the complement of brep2. See the preceding notes for the details on what "intersection" means. See the notes on gm_unary for information about computing complements.newbrep=gmunite(brep1, brep2 {, tol} );Tcl/Tk:
gmset newbrep [gmunite $brep1 $brep2 { $tol}]
Matlab:This function composes two affine transformations, and returns the composition. Thus,mat = gmcompose(mat1,mat2);Tcl/Tk:
gmset mat [gmcompose $mat1 $mat2]
result = gmapply(mat1, gmapply(mat2, obj))
should be equivalent to
result = gmapply(gmcompose(mat1, mat2), obj)
for any obj, but the latter is more efficient.
The transformations must have compatible sizes: the number of columns in the first must be one more than the number of rows in the second.
Matlab:This routine checks the correctness of a brep. The return variable is a string containing an error message, or a length-zero string if the brep is correct. See the list of correctness properties. The routine first calls the low level routineerror_string = gmcheckbrep(brep {,tol});Tcl/Tk:
gmset error_string [gmcheckbrep $brep {$tol}]
gm_verif which checks things like correct containment of
the face's point in the affine hull of the face, all boundary faces
closing, and so on. Then the routine uses
gmintersect to intersect the object with itself. This intersection should be
a copy of the original object. If not, then the original object has
two faces that meet each other improperly.
This second part of gmcheckbrep
(intersecting the brep with itself)
has cubic running time.
If the you would prefer something faster but less comprehensive,
you should call gm_verif instead.
gmget(obj)
in Matlab or gmget $obj in Tcl/Tk
prints a list of properties and values of an object. For a brep, the
properties are Type (which is the string ``brep''), EmbeddedDim,
IntrinsicDim, Level0Size, and so on up to LeveldSize, where
d is an integer that is the intrinsic dimension. There are
no values returned. Please see the documentation on breps.
For a simplicial complex, the properties are Type (which is the string ``simpcomplex''), EmbeddedDim, IntrinsicDim, NumVertices, NumSimplices, Vertices, Simplices, and SourceSpec. Please see the documentation on simplicial complexes.
The second way of calling gmget is
Matlab:Here, prop is a string that is the name of a valid property for the object (e.g.val = gmget(obj,prop);Tcl/Tk:
gmset val [gmget $obj $prop]
'IntrinsicDim') in question.
The return value is the value of this property. It may be a
string, integer, array, or matrix.
The names of the properties are not case sensitive, i.e., intrinsicdim is the same as IntrinsicDim.
gmgetf(brep,fdim,faceind) in Matlab or
gmgetf $brep $fdim $faceind in Tcl/Tk
displays all the properties and values associated with a
face of the brep, where (fdim,faceind) is a facespec.
Note that fdim must lie between 0 and the intrinsic dim of the brep and faceind must lie between 0 and LeveldSize-1, where d stands for fdim,
These properties always include the built-in properties of Children,
InternalBoundary, Affine_Coef, Affine_Rhs, and Point.
The remaining properties are
user-defined and can be inserted with the
gm_addpropval function. A
property that is meaningful for the mesh generator is
size_control. Properties that are meaningful for the
finite-element solver are bc, source and
conductivity. The color property
is meaningful for the graphics routines. The user may define additional
properties at his/her discretion.
The second way to call the routine is
Matlab:Here, prop is a string that is a property name. If the brep face in question does not have the property, then an empty string is returned. In either case, this can be tested by checking the length of val.val = gmgetf(brep,fdim,faceind,prop);Tcl/Tk:
gmset val [gmgetf $brep $fdim $faceind $prop]
Property names for faces are not case-sensitive.
The property name can be a built-in name such as affine_coef, point, affine_rhs, children, or internalboundary. It can also be numpropval, propd, or vald, to access the number of property-value pairs and the dth property value pair.
Matlab:This routine returns 1 if the brep is finite and zero if it is infinite.result = gm_isfinite(brep {, tol});Tcl/Tk:
gmset result [gm_isfinite $brep {$tol}]
Matlab:This routine takes a brep and a simplicial complex that is a mesh for that brep (generated with one of the mesh generators). For each simplex of the simplicial complex, this routine returns the lowest dimensional face of the brep containing that simplex. The return argument fspecarray is an array with one row per simplex of the simplicial complex, and two integers per row. These two integers are a facespec.fspecarray = gm_smpsrc(brep, simpcomplex {, tol});Tcl/Tk:
gmset fspecarray [gm_smpsrc $brep $simpcomplex {$tol}]
gmmeshgen, which
is either a Matlab program or Tcl/Tk program that is
a front end for the two mesh generation algorithms.
The mesh
generator is documented in a separate page.
There are two separate mesh generation algorithms in QMG, the quadtree/octree mesh generator and the Delaunay mesh generator. To directly invoke the quadtree/octree mesh generator, use the call:
Matlab:See the separate page for an explanation of these items. The Delaunay mesh generator is directly invoked with:mesh = gm_meshgen(brep, size_control, user_data, expansion_factors, logfilename, verbosity_level, gui_active {, tol});Tcl/Tk:
gmset mesh [gm_meshgen $brep $size_control $user_data $expansion_factors $logfilename $verbosity_level $gui_active {$tol}]
Matlab:It is recommended that you invoke both of these withmesh = gm_ldmeshgen(brep, dim, size_control, user_data {, min_angle {, tol} });Tcl/Tk:
gmset mesh [gm_ldmeshgen $brep $dim $size_control $user_data { $min_angle {$tol}}]
gmmeshgen
since their argument sequence may change in future releases of QMG.
After every single run of the mesh generator,
you should immediate execute gmchecktri, which is also
documented in the separate page.
A mesh can be refined; that is, each of its
simplices can be subdivided into 2^d subsimplices by gmrefine.
This routine is documented in the
other page.
The finite element solver is named gmfem.. It is
documented separately. Before calling gmfem, you
must set boundary conditions on the brep using the
gm_addpropval
routine. You must also have generated a mesh with the
gmmeshgen function. Routine gmfem and its subsidiary routines
are all written in Matlab.
In order to figure out how QMG has numbered the faces of your brep (you must know the numbering to use gm_addproval) it is very helpful to use the graphics routines described below.
Matlab:This routine produces a new brep that is the same as the old brep, except that all faces of dimension dim are colored according to a random ordering of about 20 pre-designated colors. (Just likenewbrep=gmrndcolor(brep {, dim});Tcl/Tk:
gmset newbrep [gmrndcolor $brep {$dim }]
gm_addpropval,
this routine does not change its calling argument
and therefore is useless without a return variable.)
See the graphics page for more
information about colors.
The dim argument is optional; if it is not specified, then it defaults to the embedded dimension of the brep minus 1, or the intrinsic dimension, whichever is smaller.
If a face is already colored, then gmrndcolor leaves it with the color that it has.
Matlab:This routine displays a diagram showing the colors of the faces of the brep of dimension dim. Using this routine in conjunction with gmrndcolor and gmvize is very helpful for figuring out the numbering of the faces so that you can assign boundary conditions for the finite element package.gmshowcolor(brep {, dim});Tcl/Tk
gmshowcolor $brep {$dim}
The dim argument is optional;
if it is not specified, then it defaults the same way as in
gmrndcolor.
Matlab:This routine displays a brep or simplicial complex. The display is controlled bygmviz(obj {, colorspecs, {dims {,tol}}});Tcl/Tk:
gmviz $obj {$colorspecs {$dims {$tol}}}
gmvizgui.
See the graphics page for more information
on this function.
Matlab:This routine pops up a GUI. This GUI controls the behavior of the graphics commandsgmvizguiTcl/Tk:
gmvizgui
gmviz and
gmplot. See the
graphics page for more information.
Matlab:
gmplot(scomplex, field {, solnrange {, cmap}});
The gmplot routine displays a color picture of a 2D or surface
3D finite element solution. It is available only in Matlab.
See the graphics page for more
information.
Matlab:Argument str is a string and obj is an object. This routine takes a brep or simplicial complex in Ascii form and returns the same object in chunk form. The various formats are documented in the page on geometric objects.obj = gm_in(str {, tol});Tcl/Tk:
gmset obj [gm_in $str {$tol}]
Matlab:Here, str is a string and obj is an object, either a brep or simplicial complex in chunk form. The return argument is a string. This routine converts the object from chunk format to Ascii format. For simplicial complexes, the latter two arguments have no effect. For breps, if compress is set to 1 thenstr = gm_out(obj {, compress {, tol}});Tcl/Tk:
gmset str [gm_out $obj { $compress { $tol}}]
gm_out
will omit the affine-hull property-value pairs and point
property-value pairs wherever possible.
The default is compression.
Matlab:where filename is a string and obj is an object. This routine writes a brep or simplicial complexes in Ascii format into the file usinggmwrite(obj,filename);Tcl/Tk:
gmwrite $obj $filename
gm_out with compression
enabled. The filename is first processed by gm_ofile
.
Matlab:where filename is a string and obj is an object. This filename argument is a string. This string is processed byobj = gmread(filename);Tcl/Tk:
gmset obj [gmread $filename]
gm_ifile. This routine
reads in a brep/simplicial complex in Ascii format that was saved by
the gmwrite command.
Matlab:This routine processes an input filename argument, that is, the argument tonewfilename = gm_ifile(filename);Tcl/Tk:
gmset newfilename [gm_ifile $filename]
gmread
or gmoffread.
It looks for the file in the current working directory, and if
the file is not found there, it looks in the path specified by
global variable qmg_data. This global variable is initialized to
be the environment variable QMG_DATA by startup.m in Matlab, or
by qmg_init.tcl in Tcl/Tk.
Matlab:This routine processes an output filename argument, that is, the argument tonewfilename = gm_ofile(filename);Tcl/Tk:
gmset newfilename [gm_ofile $filename]
gmwrite
or gmoffwrite.
It checks whether the file name is a relative or absolute path.
If the filename is absolute, then newfilename is set to filename.
If filename is relative, then newfilename is set to
qmg_data/filename.
This global variable is initialized to
be the environment variable QMG_DATA by startup.m in Matlab or
by qmg_init.tcl in Tcl/Tk.
Matlab:This pair of routines reads and writes breps in OFF format. The filename argument is a string. In the case of gmoffread, the filename argument is processed byTcl/Tk:brep = gmoffread(filename {,tol});
gmoffwrite(brep,filename {,tol});
gmset brep [gmoffread $filename {$tol}]
gmoffwrite $brep $filename {$tol}
gm_ifile.
In the case of gmoffwrite, it is processed by
gm_ofile.
OFF file format was designed by the Geometry Center at the University of Minnesota. This format is much simpler than QMG's Ascii format, but it also has less expressive power. With OFF format you can store only finite three-dimensional breps. No internal boundaries (either SL or MTL) are permitted, and each facet must be a simple polygon (no holes in a facet). No property-value pairs are stored, except colors can be stored in a limited manner.
In OFF format, there is a header line "OFF". The next line contains three integers, the number of vertices, the number of facets, and the number of edges. Say n is the number of vertices. The next n lines each contain three floating-point numbers which are vertex coordinates in R^3. Say m is the number of facets. The next m lines contain the specifications of the facets as sequences of integers. The first integer in a facet specification is the number of vertices in that facet, say p. The next p integers are the indices of the vertices in order around the boundary of the facet. These indices are zero-based and refer to the n coordinates. Following these p integers, there are optionally three real numbers between 0 and 1 which are an RGB color specification.
In the directory $QMG_ROOT/data shipped with QMG, the five Platonic solids are shipped in OFF-format.
Matlab:
[A,xy]=gmmpout(mesh);
This routine produces a sparse symmetric matrix A that encodes
the adjacency of the simplicial complex mesh, and a matrix
xy with the coordinate information. These two data items
A and xy can be used as input to the mesh partitioning toolbox.
This is a Matlab toolbox for partitioning meshes and computing nested
dissection orderings. For instance, to compute a nested dissection
ordering from A and xy, you would say p = geond(A,xy); where
geond is a routine in the toolbox. This permutation can then be
used with gmrenumber to renumber
a mesh.
The mesh partitioning toolbox was written by John Gilbert and Shang-Hua Teng at Xerox PARC. The geometric partitioning algorithm is based on work by Miller, Teng, Thurston and Vavasis. The matlab m-files for the toolbox are here.
Matlab:
newmesh=gmrenumber(mesh, perm {,order});
This routine renumbers the vertices of a simplicial complex
mesh according to the permutation vector perm. The permutation
vector must be a permutation of {1,...,n}, where n is the number
of vertices in the mesh. (Note: not {0,...,n-1}!). This can be
used with an ordering computed by Metis or the
mesh partitioning toolbox to get a nested dissection
ordering of the stiffness matrix.
The optional third argument indicates whether to invert the permutation. If the third argument is nonnegative (default), then the permutation is used in its forward manner, i.e., the ith vertex of newmesh is the perm(i)'th vertex of mesh. If the third argument is negative, then the permutation is used inversely, i.e., the perm(i)'th vertex of newmesh is the ith vertex of mesh.
Matlab:This routine writes out the graph adjacency matrix for a mesh into the file specified by filename. The filename is first processed bygmchacowrite(mesh,filename);Tcl/Tk:
gmchacowrite $mesh $filename
gm_ofile. This graph adjacency
data can then be used by either Chaco or Metis to partition the graph.
The file format is as follows. The first line contains two integers, the number of vertices and number of edges of the graph. Let n denote the number of vertices. Then the file has n+1 lines total. Let i (between 1 and n) be a vertex number. Then line i contains a space-delimited list of the vertices (numbered starting with 1) that are adjacent to vertex i.
Chaco was written by B. Hendrickson and R. Leland of Sandia National Laboratories, Albuquerque. Chaco is free software (at least for U.S. educational institutions), but it is not downloadable from the web. You must contact Sandia to obtain a copy. The Chaco user's guide, including information on how to obtain the software, is here in compressed format.
Metis was written by G. Karypis and V. Kumar of University of Minnesota. Metis is free software downloadable from the Metis home page.
Matlab:This routine is analogous tobrep = gmq10in(string {, tol});Tcl/Tk:
gmset brep [gmq10in $string {$tol}]
gm_in,
except that the string argument is in QMG1.0 format instead
of QMG1.1 format. The brep may not have any properties named
"affine_coef", "affine_rhs" or "point". The property name
"color" is changed from a 3-tuple to a 4-tuple by appending
a 1.
Matlab:This routine computes the Delaunay triangulation of points in the plane. The points are stored in the matrix points, which has one row per point with two entries per row. The two entries are the coordinates of the point (x,y). The routine returns a simplicial complex which is the Delaunay triangulation of the points. This routine is a "demo" rather than a shipped routine because the algorithm used is O(n^2) instead of the more efficient O(n log n) algorithms that can solve this problem.mesh = delpt(points);Tcl/Tk:
gmset mesh [delpt $points]
The script ptdel.m/ptdel.tcl runs through a demo of this routine; you click the mouse in the graphics window to trace points, then delpt is invoked to compute a triangulation, which is then displayed via gmviz.
Matlab:This routine evaluates a script file and prints the results in the specified log file. In addition, it adds time stamps at the beginning and end of each command.eval_log(scriptfilename, logfilename);Tcl/Tk:
eval_log $scriptfilename { $logfilename }
The matlab version of this routine is not able to handle multi-line constructions like 'if-then-else-end' or 'for-end'. These multi-line constructions should be expressed as a logically single line using commas and '...'. For instance, the following is OK for eval_log:
if a < 0, ... a = 0;, ... end
In the Tcl/Tk version, if the logfile is omitted then the log is displayed on the console. (This option is not necessary for Matlab because Matlab has the "echo on" feature.)
Tcl/Tk:
gmhelp cmdname
This command prints out help on a function, similar to the help
feature in matlab. In the case that the function is a Tcl procedure,
this routine prints out comments that come at the beginning of the
procedure's body. If the function is implemented in C++, then gmhelp
looks up the help information in a file called built_in_help.
Tcl/Tk:
gmset varname value
This is a C++ routine in QMG that is part of the Tcl/Tk interface. It
is the same as the built-in Tcl/Tk command set, except that it does not
produce a return value. This is useful in an interactive setting, because
typically the QMG routines return huge unreadable strings (chunk
format breps and simplicial complexes) that the user does not want
to see. The use of gmset is analogous to
terminating a Matlab assignment statement with a semicolon.
Matlab:In this call, browser and url are both strings. This command tells the browser to open the specified URL. This is used by gmviz and gmplot for notification so that 3D VRML plots appear immediately in your browser. Currently supported browsers are Netscape Navigator for Windows and Unix, and Microsoft Internet Explorer for Windows.gm_url(browser, url);Tcl/Tk:
gm_url $browser $url
This documentation is written by Stephen A. Vavasis and is copyright (c) 1996 by Cornell University. Permission to reproduce this documentation is granted provided this notice remains attached. There is no warranty of any kind on this software or its documentation. See the accompanying file 'Copyright' for a full statement of the copyright.
Stephen A. Vavasis, Computer Science Department, Cornell University, Ithaca, NY 14853, vavasis@cs.cornell.edu