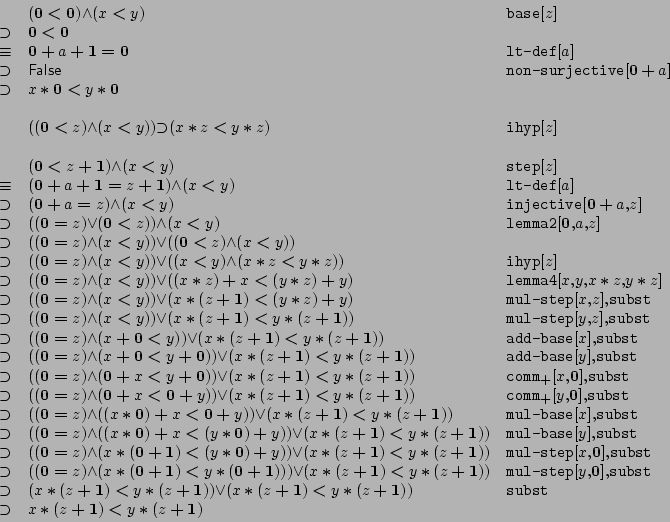
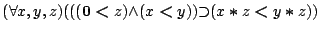- a)
- We give a finite model of a semigroup that is not commutative.
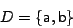
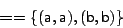
![\begin{displaymath}
\begin{array}[t]{\vert c\vert\vert c\vert c\vert}
\hline...
...thsf{b} & \mathsf{b} & \mathsf{b} \\
\hline
\end{array}
\end{displaymath}](img3.png)
Clearly, satisfies ref, sym, and
trans. Likewise,
satisfies ref, sym, and
trans. Likewise,
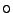 satisifies
subst, functionality, and assoc.
Hence,
satisifies
subst, functionality, and assoc.
Hence,
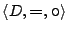 is a
semigroup. Furthermore,
is a
semigroup. Furthermore,
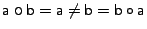 ; hence
; hence
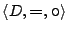 is not a
commutative semigroup.
is not a
commutative semigroup.
- b)
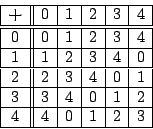
- We give a finite model of a commutative semigroup that is not a
monoid.
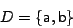
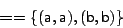
![\begin{displaymath}
\begin{array}[t]{\vert c\vert\vert c\vert c\vert}
\hline...
...thsf{b} & \mathsf{a} & \mathsf{a} \\
\hline
\end{array}
\end{displaymath}](img8.png)
Clearly,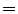 satisfies ref, sym, and
trans. Likewise,
satisfies ref, sym, and
trans. Likewise,
 satisifies
subst, functionality, assoc, and
comm. Hence,
satisifies
subst, functionality, assoc, and
comm. Hence,
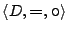 is a commutative semigroup. Furthermore,
is a commutative semigroup. Furthermore,
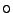 does not satisfy ident; hence
does not satisfy ident; hence
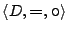 is not a monoid.
is not a monoid.
We also assume the following axiom (although it may be provable from the previous axioms):
We first prove two useful derived theorems:
- ident
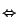 -with
-with
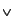 :
:
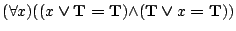
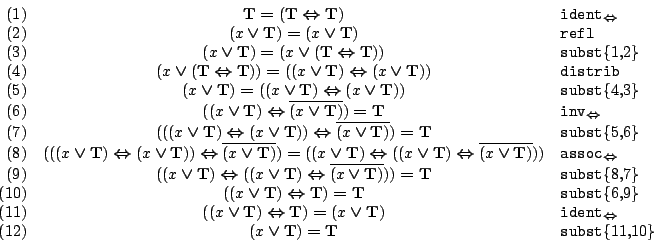
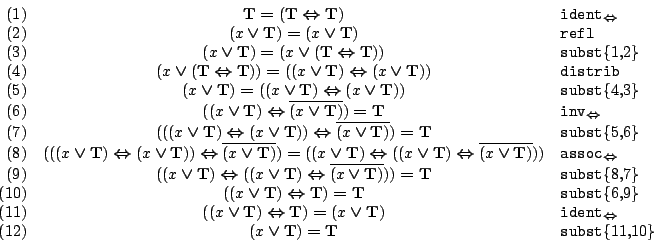
- comm
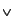 :
:
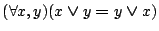

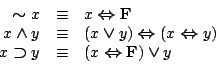
We prove the following laws using the Boolean ring axioms:
- (1)
-
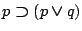
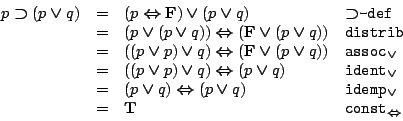
- (2)
-
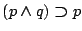

- (3)
-
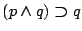
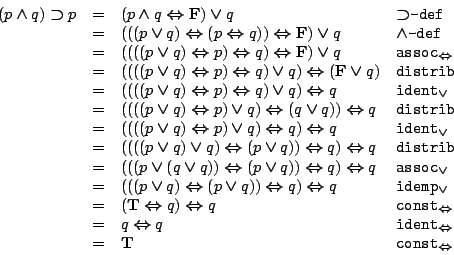
- (4)
-
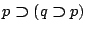
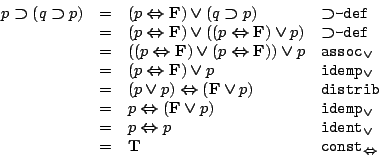
- (5)
-
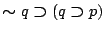
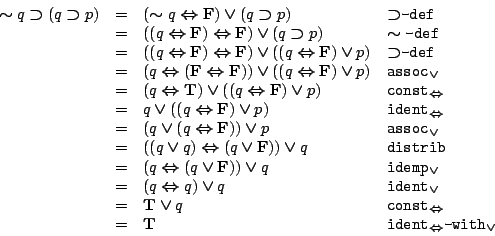
- (6)
-
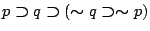
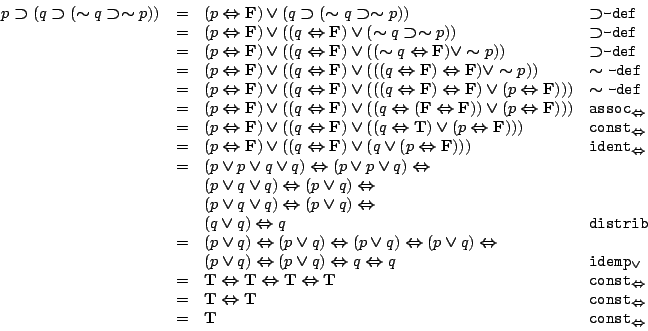
- (7)
-
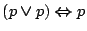
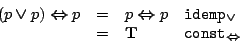
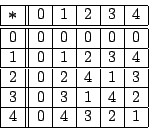
Clearly,
- lemma1:
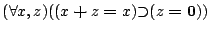

- lemma2:
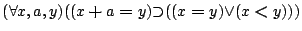
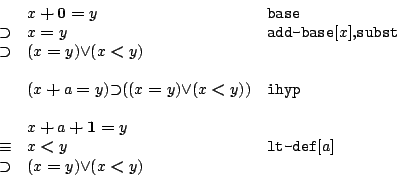
- lemma3:
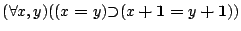
![\begin{displaymath}
\begin{array}{cll}
&
x\boldsymbol{=}y \\
\land &
...
...
\mbox{\texttt{add-base}[$y$],\texttt{subst}}
\end{array}
\end{displaymath}](img51.png)
- lemma4:
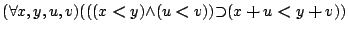
![\begin{displaymath}
\begin{array}{cll}
&
{(x\boldsymbol{<}y)}{\land }{(u\b...
...}[$a\boldsymbol{+}\mathbf{1}\boldsymbol{+}b$]}
\end{array}
\end{displaymath}](img53.png)
- lt-asym:
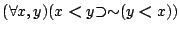

- lt-trans:
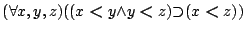
![\begin{displaymath}
\begin{array}{cll}
&
{(x\boldsymbol{<}\mathbf{0})}{\l...
...ihyp}[$z$]} \\
\supset &
x\boldsymbol{<}z
\end{array}
\end{displaymath}](img57.png)
- lt-linear:
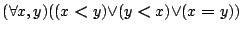
![\begin{displaymath}
\begin{array}{cll}
& &
\mbox{\texttt{base}[$x$]} \\
...
...athbf{1})} &
\mbox{\texttt{lemma3}[$x$,$y$]}
\end{array}
\end{displaymath}](img59.png)
- lt-discrete:
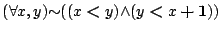

- lt-0-1:
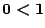
![\begin{displaymath}
\begin{array}{cll}
&
(\mathbf{0}\boldsymbol{+}\mathbf...
...bf{1} &
\mbox{\texttt{lt-def}[$\mathbf{0}$]}
\end{array}
\end{displaymath}](img63.png)
- lt-mono-+:
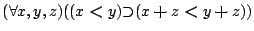
![\begin{displaymath}
\begin{array}{cll}
&
x\boldsymbol{<}y &
\mbox{\text...
...l{+}\mathbf{1} &
\mbox{\texttt{lt-def}[$a$]}
\end{array}
\end{displaymath}](img65.png)
- lt-mono-*: