-
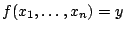 implies
implies
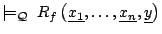 .
.
-
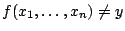 implies
implies
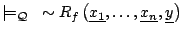 .
.
Recall that
and
- (P1)
for all
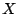 ,
if
,
if
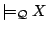 , then
, then
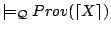
- (P2)
for all
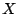 and
and 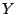 ,
,
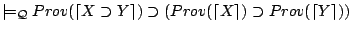
- (P3)
for all
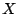 ,
,
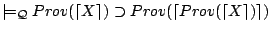
- (L)
for all
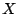 ,
if
,
if
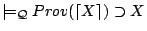 , then
, then
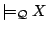
- (MP1)
for all
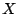 and
and 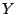 ,
if
,
if
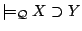 and
and
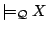 ,
then
,
then
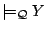
- (MP2)
for all
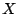 and
and 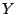 and
and 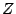 ,
if
,
if
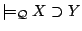 and
and
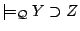 ,
then
,
then
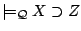
- (A1)
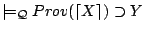 ,
by assumption.
,
by assumption.
- (A2)
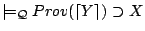 ,
by assumption.
,
by assumption.
- (B1)
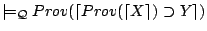 ,
by (A1) and (P1).
,
by (A1) and (P1).
- (B2)
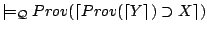 ,
by (A2) and (P1).
,
by (A2) and (P1).
- (C1)
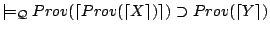 ,
by (P2), (B1), and (MP1).
,
by (P2), (B1), and (MP1).
- (C2)
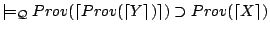 ,
by (P2), (B2), and (MP1).
,
by (P2), (B2), and (MP1).
- (D1)
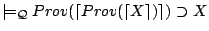 ,
by (C1), (A2), and (MP2).
,
by (C1), (A2), and (MP2).
- (D2)
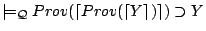 ,
by (C2), (A1), and (MP2).
,
by (C2), (A1), and (MP2).
- (E1)
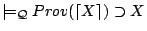 ,
by (P3), (D1), and (MP2).
,
by (P3), (D1), and (MP2).
- (E2)
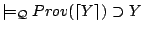 ,
by (P3), (D1), and (MP2).
,
by (P3), (D1), and (MP2).
- (F1)
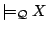 ,
by (E1) and (L).
,
by (E1) and (L).
- (F2)
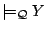 ,
by (E2) and (L).
,
by (E2) and (L).
- (a)
- We prove in
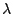 -PRL that
-PRL that
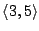 is a stamps pair.
__{{}}\
is a stamps pair.
__{{}}\
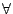 n:int. 8
n:int. 8  n
n 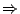
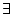 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| by induction 1 8 10 3
|
| 1. n:int
| 2. n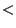 8
8
| 3. 8 n+1
n+1 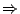
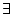 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n+1
(n+1  i * 3 + j * 5)
i * 3 + j * 5)
|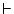 8
8  n
n 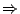
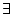 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| | by impR
|
| 4. 8 n
n
|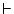
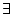 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| by arith
|
|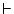 8
8  8
8 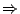
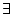 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (8
(8  i * 3 + j * 5)
i * 3 + j * 5)
| | by impR
| 1. 8 8
8
|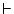
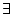 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (8
(8  i * 3 + j * 5)
i * 3 + j * 5)
| | by exR 1 1
|
|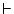 (0
(0  1)
1)  (0
(0  1)
1)  (8
(8  1 * 3 + 1 * 5)
1 * 3 + 1 * 5)
| by arith
|
|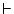 8
8  9
9 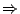
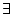 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (9
(9  i * 3 + j * 5)
i * 3 + j * 5)
| | by impR
| 1. 8 9
9
|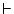
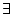 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (9
(9  i * 3 + j * 5)
i * 3 + j * 5)
| | by exR 3 0
|
|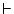 (0
(0  3)
3)  (0
(0  0)
0)  (9
(9  3 * 3 + 0 * 5)
3 * 3 + 0 * 5)
| by arith
|
|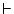 8
8  10
10 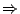
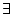 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (10
(10  i * 3 + j * 5)
i * 3 + j * 5)
| | by impR
| 1. 8 10
10
|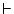
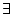 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (10
(10  i * 3 + j * 5)
i * 3 + j * 5)
| | by exR 0 2
|
|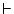 (0
(0  0)
0)  (0
(0  2)
2)  (10
(10  0 * 3 + 2 * 5)
0 * 3 + 2 * 5)
| by arith
1. n:int
2. 10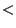 n
n
3. 8 n-3
n-3 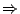
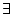 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n-3
(n-3  i * 3 + j * 5)
i * 3 + j * 5)
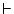 8
8  n
n 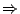
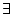 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| by impL 3
|
|
|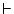 8
8  n-3
n-3
| by arith
|

3. 8 n-3
n-3
4.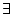 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n-3
(n-3  i * 3 + j * 5)
i * 3 + j * 5)
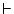 8
8  n
n 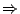
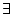 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| by exR 4
|

4. i:int
5. j:int
6. (0 i)
i)  (0
(0  j)
j)  (n-3
(n-3  i * 3 + j * 5)
i * 3 + j * 5)
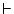 8
8  n
n 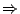
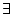 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| by andL 6

6. 0 i
i
7. 0 j
j
8. n-3 i * 3 + j * 5
i * 3 + j * 5
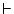 8
8  n
n 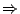
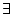 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| by impR

9. 8 n
n
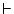
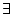 i,j:int. (0
i,j:int. (0  i)
i)  (0
(0  j)
j)  (n
(n  i * 3 + j * 5)
i * 3 + j * 5)
| by exR i+1,j

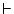 (0
(0  i+1)
i+1)  (0
(0  j)
j)  (n
(n  (i+1) * 3 + j * 5)
(i+1) * 3 + j * 5)
by arith
- (b)
- We describe the algorithm implicitly contained in the proof of
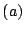 in
in 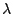 -PRL notation.
__{{}}\
-PRL notation.
__{{}}\stampsi(n:int):int
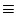 n => 0
n => 0
8 => 1
9 => 3
10 => 0
n => stampsi(n-3) + 1
stampsj(n:int):int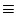 n => 0
n => 0
8 => 1
9 => 0
10 => 2
n => stampsj(n-3) - (c)
- If
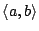 is a stamps pair (such that
is a stamps pair (such that 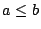 ), then
), then
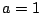 , or
, or
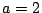 and
and
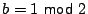 , or
, or
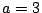 and
and 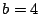 , or
, or
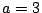 and
and 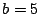
__{{}}\
We give al:list. (
(l=[])
i:int. (i
l
j:int. (j
l
j
i)))
__{{}}\
iWe prove the above statementl
k:int. (index(k,l)=i
0
k
k
length(l))
__{{}}\
We describe the extracted algorithm inl:list. (
(l=[])
i:int. (i
l
j:int. (j
l
j
i)))
| by induction x::l
|
|([]=[])
i:int. (i
[]
j:int. (j
[]
j
i))
| | by impR
| 1.([]=[])
|i:int. (i
[]
j:int. (j
[]
j
i))
| | by notL 1
|
|[]=[]
| by equality
|
| 1. x:int
|([x]=[])
i:int. (i
[x]
j:int. (j
[x]
j
i))
| | by impR
|
| 2.([x]=[])
|i:int. (i
[x]
j:int. (j
[x]
j
i))
| | by exR x
|
|x
[x]
j:int. (j
[x]
j
x)
| | by andR
| |
| |
| |x
[x]
| | | by unfoldin 0
| |
| |k:int. (index(k,[x])=i
0
k
k
length([x]))
| | | by exR 0
| |
| |index(0,[x])=x
0
0
0
length([x])
| | | by simplify in 0
| |
| |x=x
0
0
0
1 | | by arith

|
|
|j:int. (j
[x]
j
x)
| | by allR
|
| 3. j:int
|j
[x]
j
x
| | by impR
| |
|
| 4. j[x]
|j
x
| | by unfoldin 4
|
| 4.k:int. (index(k,[x])=j
0
k
k
length([x]))
|j
x
| | by exL 4
| |
|
| 4. k:int
| 5. index(k,[x])=j0
k
k
length([x])
|j
x
| | by simplify in 5
|
| 5. index(k,[x])=j0
k
k
1
|j
x
| | by andL 5
|
| 5. index(k,[x])=j
| 6. 0k
| 7. k1
|j
x
| | by cut k=0
| |
| |
| |k=0
| | by arith
|
|
| 8. k=0
|j
x
| | by cut index(k,[x])=j
| |
| |
| |index(k,[x])=j
| | by hyp 5
|
|
| 9. index(k,[x])=j
|j
x
| | by subst 8 9
|
| 9. index(0,[x])=j
|j
x
| | by simplify 9
|
| 9. x=j
|j
x
| by arith
1. x:int
2. l:list
3.(l=[])
i:int. (i
l
j:int. (j
l
j
i))
(x::l=[])
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by cut (l=[])(l=[])
|
|
|(l=[])
(l=[])
| by equality

4. (l=[])(l=[])
(x::l=[])
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by orL 4
|
|
| 4. l=[]
|(x::l=[])
i:int. (i
x::l
j:int. (j
x::l
j
i))
| | by subst 4 0
|
|i:int. (i
x::[]
j:int. (j
x::[]
j
i))
| | by simplify 0
| |
|
|i:int. (i
[x]
j:int. (j
[x]
j
i))
| by proof of previous case
|

4.(l=[])
(x::l=[])
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by impR

5.(x::l=[])
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by impL 3
|
|
|(l=[])
| by hyp 4

3.(l=[])
4.(x::l=[])
5.(l=[])
6.i:int. (i
l
j:int. (j
l
j
i))
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by exL 6

6. i:int
7. il
j:int. (j
l
j
i)
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by andL 7

7. il
8.j:int. (j
l
j
i)
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by unfold7

7.k:int. (index(k,l)=i
0
k
k
length(x::l))
8.j:int. (j
l
j
i)
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by exL 7

7. k:int
8. index(k,l)=i0
k
k
length(x::l)
9.j:int. (j
l
j
i)
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by andL 8

8. index(k,l)=i
9. 0k
10. klength(x::l)
11.j:int. (j
l
j
i)
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by simplify 10

8. index(k,l)=i
9. 0k
10. klength(l)+1
11.j:int. (j
l
j
i)
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by cut (xi)
(x
i)
|
|
|(x
i)
(x
i)
| by arith
|

12. (xi)
(x
i)
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by orL 12
|
|
| 12. xi
|i:int. (i
x::l
j:int. (j
x::l
j
i))
| | by exR i
|
|i
x::l
j:int. (j
x::l
j
i)
| | by andR
| |
| |
| |i
x::l
| | | by unfoldin 0
| |
| |k:int. (index(k,x::l)=i
0
k
k
length(x::l))
| | | by exR k+1
| |
| |index(k+1,x::l)=i
0
k+1
k+1
length(x::l)
| | | by def index(k+1,x::l) up
| | |
| | |
| | |0
k+1
| | | by arith
| |
| |
| | 13. 0k+1
| | 14. index(k+1,x::l) = index(k+1-1,tl(x::l))
| |index(k+1,x::l)=i
0
k+1
k+1
length(x::l)
| | | by subst 14 0
| |
| |index(k+1-1,tl(x::l))=i
0
k+1
k+1
length(x::l)
| | | by simplify 0
| |
| |index(k,l)=i
0
k+1
k+1
length(l)+1
| | by arith
|
|
|j:int. (j
x::l
j
i)
| | by allR
|
| 13. j: int
|j
x::l
j
i
| | by impR
|
| 14. jx::l
|j
i
| | by unfoldin 14
|
| 14.k:int. (index(k,x::l)=j
0
k
k
length(x::l))
|j
i
| | exL 14
|
| 14. k':int
| 15. index(k',x::l)=j0
k'
k'
length(x::l))
|j
i
| | andL 15
| |
|
| 15. index(k',x::l)=j
| 16. 0k'
| 17. k'length(x::l))
|j
i
| | by simplify 17
|
| 17. k'length(l)+1
|j
i
| | cut k'=0k'
0
| |
| |
| |k'=0
k'
0
| | by arith
|
|
| 18. k'=0k'
0
|j
i
| | by orL 18
| |
| |
| | 18. k'=0
| |j
i
| | | by cut index(k',x::l)=j
| | |
| | |
| | |index(k',x::l)=j
| | | by hyp 15
| |
| |
| | 19. index(k',x::l)=j
| |j
i
| | | by subst 18 19
| |
| | 19. index(0,x::l)=j
| |j
i
| | | by simplify 19
| |
| | 19. x=j
| |j
i
| | by arith
|
|
| 18. k'0
|j
i
| | by allL 11 j
|
| 19. jl
j
i
|j
i
| | by impL 19
| |
| |
| |j
l
| | | by unfoldin 0
| |
| |k:int. (index(k,l)=j
0
k
k
length(l))
| | | by exR k'-1
| |
| |index(k'-1,l)=j
0
k'-1
k'-1
length(l)
| | | by def index(k',x::l) up
| | |
| | |
| | |0
k'
| | | by hyp 18
| | |
| |
| |
| | 20. 0k'
| | 21. index(k',x::l) = index(k'-1,tl(x::l))
| |index(k'-1,l)=j
0
k'-1
k'-1
length(l)
| | | by simplify 21
| |
| | 21. index(k',x::l) = index(k'-1,l)
| |index(k'-1,l)=j
0
k'-1
k'-1
length(l)
| | by arith
|
| 19. jl
| 20. ji
|j
i
| by hyp 20

12. xi
i:int. (i
x::l
j:int. (j
x::l
j
i))
| by exR x

x
x::l
j:int. (j
x::l
j
x)
| by andR
|
|
|x
x::l
| | by unfoldin 0
|
|k:int. (index(k,x::l)=x
0
k
k
length(x::l))
| | by exR 0
|
|index(0,x::l)=x
0
0
0
length(x::l)
| | by simplify 0
|
|x=x
0
0
0
length(l)+1
| by arith

j:int. (j
x::l
j
x)
| by allR

13. j:int
j
x::l
j
x
| by impR

14. jx::l
j
x
| by unfoldin 14

14.k:int. (index(k,x::l)=j
0
k
k
length(x::l))
j
x
| by exL 14

14. k':int
15. index(k',x::l)=j0
k'
k'
length(x::l)
j
x
| by andL 15

15. index(k',x::l)=j
16. 0k'
17. k'length(x::l)
j
x
| by simplify 17
|

17. k'length(l)+1
j
x
| by cut k'=0k'
0
|
|
|k'=0
k'
0
| by arith

18. k'=0k'
0
j
x
| by orL 18
|
|
| 18. k'=0
|j
x
| | by cut index(k',x::l)=j
| |
| |
| |index(k',x::l)=j
| | by hyp 15
|
|
| 19. index(k',x::l)=j
|j
x
| | by subst 18 19
|
| 19. index(0,x::l)=j
|j
x
| | by simplify 19
|
| 19. x=j
|j
x
| by arith

18. k'0
j
x
| by allL 11 j

19. jl
j
i
j
x
| by impL 19
|
|
|j
l
| | by unfoldin 0
|
|k:int. (index(k,l)=j
0
k
k
length(l))
| | exR k'-1
|
|index(k'-1,l)=j
0
k'-1
k'-1
length(l))
| | by def index(k',x::l) up
| |
| |
| |0
k'
| | by hyp 18
|
|
| 20. 0k'
| 21. index(k',x::l) = index(k'-1,tl(x::l))
|index(k'-1,l)=j
0
k'-1
k'-1
length(l))
| | by simplify 21
| |
|
| 20. 0k'
| 21. index(k',x::l) = index(k'-1,l)
|index(k'-1,l)=j
0
k'-1
k'-1
length(l))
| by arith

19. jl
20. ji
j
x
by arith
__{{}}\
listmax(l:list):int0 => 0
1 => hd(l)
l => if tl(l)[]
then hd(l)
else if hd(l)listmax(tl(l))
then listmax(tl(l))
else hd(l)