Problem Set 5
Due Date: Thurs, Feb 27
Please study Smullyan, Chapter XI, p. 101-108, and skim Chapter IV, p. 43-51 for Thurs, Feb 27.
- Give a top-down Gentzen proof of formulas (2), (4), (6), and (8) on
page 24.
- Recall the lecture presentation of Smullyan's definition of a tree. A
tree is a 4-tuple
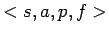 where
where 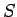 is a set of nodes,
is a set of nodes, 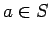 ,
, 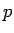 maps
maps
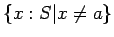 into
into 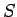 ; it computes the predecessor of a node, the
function
; it computes the predecessor of a node, the
function 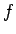 maps
maps 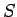 to
to
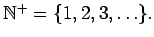 The two axioms are:
The two axioms are:
Ax 1. For all 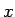 in in 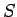 , , 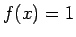 iff iff 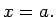 |
Ax 2. For all 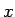 in in 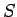 , ,
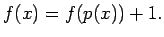 |
Define
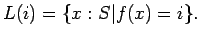
Prove carefully that
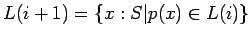 and describe the result
graphically.
and describe the result
graphically.
- Recall that Refinement Logic is a single conclusion (top down)
Gentzen system in which the rule
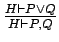 is
replaced by
is
replaced by
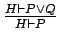 or
or
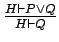 and the rule
and the rule
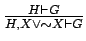 for any formula
for any formula 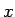 .
.
Prove the following formulas in Refinement Logic:
-
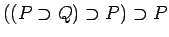
-
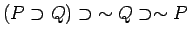
-
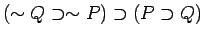
-
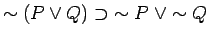
- Write down the rules for a Gentzen system based on the Sheffer stroke
and one based on joint denial (see p. 14 of Smullyan and p.30).
- Produce Tableau rules and Refinement rules for a logic with the
constants
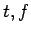 (Smullyan, p. 13), but without
(Smullyan, p. 13), but without 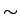 . Define
. Define 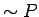 as
as 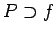 and show how to replace any deduction using the
and show how to replace any deduction using the 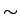 rules by
one using
rules by
one using 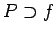 instead.
instead.
Juanita Heyerman
2003-02-27
![]()
![]() and describe the result
graphically.
and describe the result
graphically.
![]()
![]() and describe the result
graphically.
and describe the result
graphically.