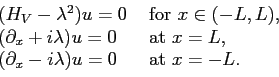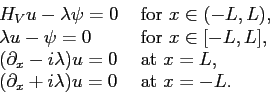Resonance computations and nonlinear eigenproblems
In this section we describe the ideas behind the codes for squarepot.m and splinepot.m.
If the support of ![]() is contained in a compact interval
is contained in a compact interval ![]() ,
we can compute both resonance solutions and ordinary eigenvalues of the
Schrödinger problem (8) by writing appropriate boundary
conditions at
,
we can compute both resonance solutions and ordinary eigenvalues of the
Schrödinger problem (8) by writing appropriate boundary
conditions at ![]() :
:
In terms of
We now discretize the boundary and domain operators to get a finite-dimensional generalized eigenvalue problem. For small discretizations with up to a few hundred unknowns, we can solve this generalized eigenvalue problem using MATLAB's eig command, which uses the dense eigensolvers in LAPACK [2]. For larger discretizations, we use MATLAB's eigs to call ARPACK, a standard Arnoldi-based iterative eigensolver [19].
For the calculations shown in this note, we used a high-order
pseudospectral collocation method to discretize the
operators [33], [5]. We partition the support
interval ![]() into subintervals, and approximate
into subintervals, and approximate ![]() by a
high-order polynomial on each subinterval. At the Chebyshev points on
the interior of each subinterval, we insist that the domain
differential equations be satisfied exactly, while at the junctions
between neighboring intervals, we insist that the solution
by a
high-order polynomial on each subinterval. At the Chebyshev points on
the interior of each subinterval, we insist that the domain
differential equations be satisfied exactly, while at the junctions
between neighboring intervals, we insist that the solution ![]() and the
first derivative
and the
first derivative
![]() must both be continuous. Assuming
that the potential is smooth except possibly at the endpoints of the
subintervals, the collocation scheme we use is spectrally
accurate; that is, the error asymptotically decreases faster than
any algebraic function of the order of the collocation scheme. As a
simple check on the accuracy of the computed eigenvalues of
(31), we increase the order of the method by 50%,
recompute the eigenvalues, and compare the results obtained from the
coarser and the finer discretization.
must both be continuous. Assuming
that the potential is smooth except possibly at the endpoints of the
subintervals, the collocation scheme we use is spectrally
accurate; that is, the error asymptotically decreases faster than
any algebraic function of the order of the collocation scheme. As a
simple check on the accuracy of the computed eigenvalues of
(31), we increase the order of the method by 50%,
recompute the eigenvalues, and compare the results obtained from the
coarser and the finer discretization.
We can write the analogue of (30) in higher dimensions,
with a Dirichlet-to-Neumann (DtN) map - or some approximation to a
DtN map - in place of the boundary conditions at ![]() . In more
than one space dimension, this boundary map ceases to be a linear
function of
. In more
than one space dimension, this boundary map ceases to be a linear
function of ![]() , and so we cannot easily convert the problem
into a linear eigenvalue problem. Researchers are studying these more
complicated nonlinear eigenvalue problems for a variety of
engineering problems [3]. Many of these problems involve
resonances in models of elastic, acoustic, or electromagnetic
resonators with radiation losses.
, and so we cannot easily convert the problem
into a linear eigenvalue problem. Researchers are studying these more
complicated nonlinear eigenvalue problems for a variety of
engineering problems [3]. Many of these problems involve
resonances in models of elastic, acoustic, or electromagnetic
resonators with radiation losses.
David Bindel 2006-10-04